题目内容
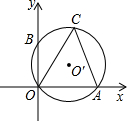 如图,CO、CA是⊙O′的弦,⊙O′与坐标系x、y轴分别交于点A、B,B点坐标为(0,2),∠ACO=60°,则⊙O′的直径为( )
如图,CO、CA是⊙O′的弦,⊙O′与坐标系x、y轴分别交于点A、B,B点坐标为(0,2),∠ACO=60°,则⊙O′的直径为( )| A、2 | ||
B、
| ||
| C、4 | ||
| D、5 |
考点:圆周角定理,坐标与图形性质,垂径定理
专题:
分析:连接AB,由圆周角定理可知AB为圆的直径,解直角三角形OBA求出AB的长即可.
解答: 解:连接AB,
解:连接AB,
∵∠AOB=90°,
∴AB是圆的直径,
∵∠ACO=60°,
∴∠OBA=60°,
∵OB=2,
∴AB=4,
故选C.
 解:连接AB,
解:连接AB,∵∠AOB=90°,
∴AB是圆的直径,
∵∠ACO=60°,
∴∠OBA=60°,
∵OB=2,
∴AB=4,
故选C.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12的算术平方根介于( )
| A、5和4之间 |
| B、4与3之间 |
| C、3与2之间 |
| D、2与1之间 |
⊙O1与⊙O2半径是方程x2-7x+12=0两根,且O1O2=0.5,则两圆的位置关系为( )
| A、外离 | B、外切 | C、内切 | D、内含 |
下列合并同类项,正确的是( )
| A、2a+b=2ab |
| B、2a-a=2 |
| C、3a2+2a2=5a4 |
| D、2a2b-a2b=a2b |
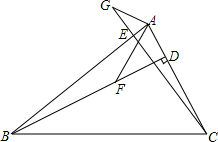 已知:BD,CE是△ABC的高,点F在BD上,BF=AC,点G在CE的延长线上,CG=AB.
已知:BD,CE是△ABC的高,点F在BD上,BF=AC,点G在CE的延长线上,CG=AB.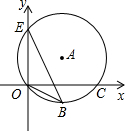 如图,点E(0,4),O(0,0),C(5,0)在⊙A上,BE是⊙A上的一条弦,则cos∠OBE=
如图,点E(0,4),O(0,0),C(5,0)在⊙A上,BE是⊙A上的一条弦,则cos∠OBE=