题目内容
20．先化简，再求值：$\frac{{a}^{2}-1}{{b}^{2}-2b+1}$÷$\frac{a+1}{b-1}$+$\frac{1}{b-1}$，其中a=$\sqrt{3}$，b=$\sqrt{3}$+1．分析 先根据分式的混合运算顺序和法则化简原式，再将a、b的值代入求解可得．
解答 解：原式=$\frac{（a-1）（a+1）}{（b-1）^{2}}$•$\frac{b-1}{a+1}$+$\frac{1}{b-1}$
=$\frac{a-1}{b-1}$+$\frac{1}{b-1}$
=$\frac{a}{b-1}$，
当a=$\sqrt{3}$，b=$\sqrt{3}$+1时，
原式=$\frac{\sqrt{3}}{\sqrt{3}+1-1}$=1．
点评 本题主要考查分式的化简求值，熟练掌握分式的混合运算顺序和法则是解题的关键．
练习册系列答案
相关题目
10．
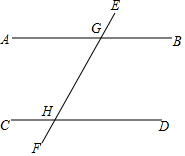已知直线AB∥CD，EF交AB于G，交CD于H，若∠BGH的度数比∠GHD的2倍多10°，设∠BGH和∠GHD的度数分别为x、y，则下列正确的方程组为（ ）
已知直线AB∥CD，EF交AB于G，交CD于H，若∠BGH的度数比∠GHD的2倍多10°，设∠BGH和∠GHD的度数分别为x、y，则下列正确的方程组为（ ）| A． | $\left\{\begin{array}{l}{x+y=180°}\\{x=y+10°}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+y=180°}\\{x=2y+10°}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{x+y=180°}\\{x=2y-10°}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x+y=180°}\\{y=2x+10°}\end{array}\right.$ |
15．某校举办演讲比赛，对参赛20名选手的得分m（满分10分）进行分组统计，统计结果如表所示：
（1）求a的值；
（2）若用扇形图来描述，求分值在8≤m＜9范围内所对应的扇形图的圆心角大小；
（3）将在第一组内的两名选手记为：A1、A2，在第四组内的两名选手记为：B1、B2，现从第一组和第四组中随机选取2名选手进行座谈，用树状图或列表法列出所有可能结果，并求第一组至少有1名选手被选中的概率．
| 组号 | 分值 | 频数 |
| 一 | 6≤m＜7 | 2 |
| 二 | 7≤m＜8 | 8 |
| 三 | 8≤m＜9 | a |
| 四 | 9≤m≤10 | 2 |
（2）若用扇形图来描述，求分值在8≤m＜9范围内所对应的扇形图的圆心角大小；
（3）将在第一组内的两名选手记为：A1、A2，在第四组内的两名选手记为：B1、B2，现从第一组和第四组中随机选取2名选手进行座谈，用树状图或列表法列出所有可能结果，并求第一组至少有1名选手被选中的概率．
5．如图是某几何体的三视图及相关数据，下列各式中正确的是（ ）
| A． | a＞c | B． | a2+b2=c2 | C． | 4a2+b2=c2 | D． | b＞c |
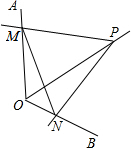如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：（1）PM=PN恒成立；（2）OM+ON的值不变；（3）四边形PMON的面积不变；（4）MN的长不变，其中正确的个数为（ ）
