题目内容
15.某校举办演讲比赛,对参赛20名选手的得分m(满分10分)进行分组统计,统计结果如表所示:| 组号 | 分值 | 频数 |
| 一 | 6≤m<7 | 2 |
| 二 | 7≤m<8 | 8 |
| 三 | 8≤m<9 | a |
| 四 | 9≤m≤10 | 2 |
(2)若用扇形图来描述,求分值在8≤m<9范围内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2,在第四组内的两名选手记为:B1、B2,现从第一组和第四组中随机选取2名选手进行座谈,用树状图或列表法列出所有可能结果,并求第一组至少有1名选手被选中的概率.
分析 (1)根据被调查人数为20和表格中的数据可以求得a的值;
(2)360°乘以8≤m<9人数所占比例;
(3)根据题意可以写出所有的可能性,从而可以得到第一组至少有1名选手被选中的概率.
解答 解:(1)a=20-(2+8+2)=8;
(2)360°×$\frac{8}{20}$=144°,
答:分值在8≤m<9范围内所对应的扇形图的圆心角为144°;
(3)由题意可得,所有的可能性如下图所示,
故第一组至少有1名选手被选中的概率是:$\frac{10}{12}$=$\frac{5}{6}$.
点评 本题考查列表法与树状图法、频数分布表、扇形统计图,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
 如图,学校将一面积为240m2的矩形空地一边增加4m,另一边增加5m后,建成了一个正方形训练场,则此训练场的面积为400m2.
如图,学校将一面积为240m2的矩形空地一边增加4m,另一边增加5m后,建成了一个正方形训练场,则此训练场的面积为400m2.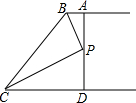 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,若AD=8,则点P到BC的距离是4.
如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,若AD=8,则点P到BC的距离是4.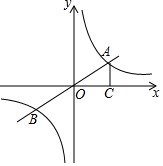 如图,直线y=kx(k为常数,k≠0)与双曲线y=$\frac{m}{x}$(m为常数,m>0)的交点为A、B,AC⊥x轴于点C,∠AOC=30°,OA=2.
如图,直线y=kx(k为常数,k≠0)与双曲线y=$\frac{m}{x}$(m为常数,m>0)的交点为A、B,AC⊥x轴于点C,∠AOC=30°,OA=2.