题目内容
11．已知一次函数y=mx+n（m、n为常数，且m、n≠0）．求此一次函数的图象经过第一象限的概率是$\frac{3}{4}$．分析 根据m，n的符号，画树状图，根据所得的结果进行计算，即可得到一次函数的图象经过第一象限的概率．
解答 解：根据m、n为常数，且m、n≠0，画树状图可得：
总共有4种等可能的情况，其中一次函数的图象经过第一象限的有3种，
∴一次函数的图象经过第一象限的概率是$\frac{3}{4}$，
故答案为：$\frac{3}{4}$．
点评 本题主要考查了概率的计算以及一次函数图象与系数的关系，解题时注意：直线y=kx+b与y轴交于（0，b），当b＞0时，（0，b）在y轴的正半轴上，直线与y轴交于正半轴；当b＜0时，（0，b）在y轴的负半轴，直线与y轴交于负半轴．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
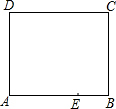如图是一张长方形纸片ABCD，已知AB=8，AD=7，E为AB上的一点，AE=5，点P在长方形ABCD的一边上，要使△AEP是等腰三角形，则△AEP的底边长为5或5$\sqrt{2}$或4$\sqrt{5}$．
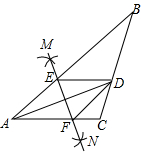如图，在△ABC中，AD平分∠BAC，按如下步骤作图：①分别以点A、D为圆心，以大于$\frac{1}{2}$AD的长为半径在AD两侧作弧，交于两点M、N；②连接MN分别交AB、AC于点E、F；③连接DE、DF．若BD=6，AF=4，CD=3，则下列说法中正确的是（ ）
如图，点C在线段AB的延长线上，BC=2AB，点D是线段AC的中点，AB=2cm，则BD的长度是1cm．