题目内容
5.计算:①3+(-3)=0; ②-2+4=2;
③2比-2大4; ④-8--16=8;
⑤-1-(-1)2=-2; ⑥-32×$\frac{2}{9}$=-2.
分析 ①根据有理数的加法法则进行计算即可;
②根据有理数的加减法则进行计算即可;
③根据题意列出有理数相减的式子,进而可得出结论;
④根据有理数的减法法则进行计算即可;
⑤先算乘方,再算加减即可;
⑥先算乘方,再算乘法即可.
解答 解:①3-3=0.
故答案为:0;
②-2+4=2.
故答案为:4;
③2-(-2)=4.
故答案为:4;
④-8-(-16)=8.
故答案为:-16;
⑤原式=-1-1=-2.
故答案为:-2;
⑥原式=-9×$\frac{2}{9}$=-2.
故答案为:-2.
点评 本题考查的是有理数的混合运算,熟知有理数混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
14.对于任意不相等的两个实数a、b,定义运算※如下:a※b=$\frac{\sqrt{a+b}}{a-b}$;例如3※2=$\frac{\sqrt{3+2}}{3-2}$=$\sqrt{5}$.那么5※7等于( )
| A. | $-\sqrt{3}$ | B. | -4 | C. | $-2\sqrt{3}$ | D. | -3 |
15.若函数y=$\frac{x-2}{{x}^{2}-1}$的函数值为0,则自变量x的值为( )
| A. | 2 | B. | -1 | C. | ±1 | D. | 1 |
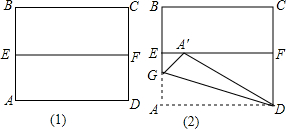 如图1,四边形ABCD是一张正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展平,然后沿直线DG折叠,使A点落在EF上,对应点为A′,求∠DA′F的度数.
如图1,四边形ABCD是一张正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展平,然后沿直线DG折叠,使A点落在EF上,对应点为A′,求∠DA′F的度数. 如图,△ABC的三个顶点分别在小正方形的顶点(格点)上,称格点三角形,在图中能画出3个不同的格点三角形(除△ABC外),使它能与△ABC全等.
如图,△ABC的三个顶点分别在小正方形的顶点(格点)上,称格点三角形,在图中能画出3个不同的格点三角形(除△ABC外),使它能与△ABC全等. 如图,在△ABC中,∠C=90°,AD平分∠CAB,交BC于点D,CD=15cm,则点D到AB的距离是15cm.
如图,在△ABC中,∠C=90°,AD平分∠CAB,交BC于点D,CD=15cm,则点D到AB的距离是15cm. 如图所示,是由5个大小相同的立方体搭起来的一个几何体,则从左面看到的它的形状图是( )
如图所示,是由5个大小相同的立方体搭起来的一个几何体,则从左面看到的它的形状图是( )


