题目内容
18．已知$\sqrt{24a}$是整数，a是正整数，a的最小值是（ ）| A． | 0 | B． | 3 | C． | 6 | D． | 24 |
分析 因为$\sqrt{24a}$是整数，且$\sqrt{24a}=2\sqrt{6a}$，则6a是完全平方数，满足条件的最小正整数a为6．
解答 解：∵$\sqrt{24a}=2\sqrt{6a}$，且$\sqrt{24a}$是整数，
∴$2\sqrt{6a}$是整数，即6a是完全平方数；
∴a的最小正整数值为6．
故选C．
点评 主要考查了乘除法法则和二次根式有意义的条件．二次根式有意义的条件是被开方数是非负数．把12分解成平方数与另一个因数相乘的形式是解题的关键．
练习册系列答案
相关题目
在菱形ABCD中，E为AB的中点，OE=5，则菱形ABCD的边长为10．
6．
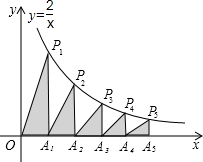如图，在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5，过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数y=$\frac{2}{x}$（x≠0）的图象相交于点P1、P2、P3、P4、P5，得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5，并设其面积分别为S1、S2、S3、S4、S5，则S5的值为（ ）
如图，在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5，过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数y=$\frac{2}{x}$（x≠0）的图象相交于点P1、P2、P3、P4、P5，得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5，并设其面积分别为S1、S2、S3、S4、S5，则S5的值为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{5}$ |
13．已知直角三角形的两条直角边的边长为3和4，则它的斜边长C是（ ）
| A． | 5 | B． | $\sqrt{7}$ | C． | 5或$\sqrt{7}$ | D． | 1＜C＜7 |
10．$\sqrt{2}$的相反数是（ ）
| A． | -$\sqrt{2}$ | B． | $\sqrt{2}$ | C． | -2 | D． | $\frac{\sqrt{2}}{2}$ |
7．下列多边形中，能够铺满地面的是（ ）
| A． | 正方形 | B． | 正五边形 | C． | 正七边形 | D． | 正八边形 |
