题目内容
8.如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q与B不重合),过P作PE⊥AB于E,连接PQ交AB于D(1)当∠BQD=30°时,求AP的长;
(2)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由;
(3)在整个运动过程中,设AP为x,BD为y,求y关于x的函数关系式,并写出自变量x的取值范围.
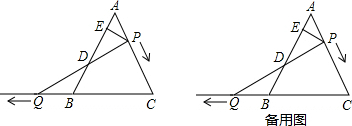
分析 (1)由△ABC是边长为6的等边三角形,可知∠ACB=60°,再由∠BQD=30°可知∠QPC=90°,设AP=x,则PC=6-x,QB=x,在Rt△QCP中,∠BQD=30°,PC=$\frac{1}{2}$QC,即6-x=$\frac{1}{2}$(6+x),求出x的值即可;
(2)作QF⊥AB,交直线AB于点F,连接QE,PF,由点P、Q做匀速运动且速度相同,可知AP=BQ,再根据全等三角形的判定定理得出△APE≌△BQF,再由AE=BF,PE=QF且PE∥QF,可知四边形PEQF是平行四边形,进而可得出EB+AE=BE+BF=AB,DE=$\frac{1}{2}$AB,由等边△ABC的边长为6可得出DE=3,故当点P、Q运动时,线段DE的长度不会改变.
(3)根据AP=x,BD=y,得出AE=$\frac{1}{2}$x,得出关系式即可.
解答 解:(1)∵△ABC是边长为6的等边三角形,
∴∠ACB=60°,
∵∠BQD=30°,
∴∠QPC=90°,
设AP=x,则PC=6-x,QB=x,
∴QC=QB+BC=6+x,
∵在Rt△QCP中,∠BQD=30°,
∴PC=$\frac{1}{2}$QC,即6-x=$\frac{1}{2}$(6+x),解得x=2,
∴AP=2;
(2)当点P、Q同时运动且速度相同时,线段DE的长度不会改变.理由如下:
作QF⊥AB,交直线AB于点F,连接QE,PF,
又∵PE⊥AB于E,
∴∠DFQ=∠AEP=90°,
∵点P、Q速度相同,
∴AP=BQ,
∵△ABC是等边三角形,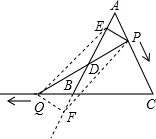
∴∠A=∠ABC=∠FBQ=60°,
在△APE和△BQF中,
∵∠AEP=∠BFQ=90°,
∴∠APE=∠BQF,
在△APE与△BQF中,
$\left\{\begin{array}{l}{∠AEP=∠BFQ}\\{∠A=∠FBQ}\\{AP=BQ}\end{array}\right.$,
∴△APE≌△BQF(AAS),
∴AE=BF,PE=QF且PE∥QF,
∴四边形PEQF是平行四边形,
∴DE=$\frac{1}{2}$EF,
∵EB+AE=BE+BF=AB,
∴DE=$\frac{1}{2}$AB,
又∵等边△ABC的边长为6,
∴DE=3,
∴点P、Q同时运动且速度相同时,线段DE的长度不会改变;
(3)△APE中,∠APE=30°,AE=$\frac{1}{2}$x,
可得:$\frac{1}{2}x+3+y=6$,
y=$-\frac{1}{2}x+3$;
自变量的取值范围为:0<x<6.
点评 本题考查的是等边三角形的性质及全等三角形的判定定理、平行四边形的判定与性质,根据题意作出辅助线构造出全等三角形是解答此题的关键.

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案| A. | 0 | B. | 3 | C. | 6 | D. | 24 |
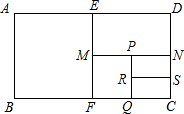 如图,在矩形ABCD中,AB=a,将矩形ABCD沿EF对折后,得ABFE和矩形EFCD,然后再把其中的一个矩形EFCD沿MN对折,得矩形MNCF和矩形MNDE,…,依此类推,得矩形PRSN和RQCS,并且所有矩形都相似,则RS等于( )
如图,在矩形ABCD中,AB=a,将矩形ABCD沿EF对折后,得ABFE和矩形EFCD,然后再把其中的一个矩形EFCD沿MN对折,得矩形MNCF和矩形MNDE,…,依此类推,得矩形PRSN和RQCS,并且所有矩形都相似,则RS等于( )| A. | $\frac{\sqrt{2}}{8}$a | B. | $\frac{\sqrt{2}}{4}$a | C. | $\frac{\sqrt{2}}{2}$a | D. | $\frac{1}{4}$a |
 如图,抛物线y=ax2+bx+c与坐标轴的交点为A、B、C,且OA=OC=1,则下列关系中正确的是( )
如图,抛物线y=ax2+bx+c与坐标轴的交点为A、B、C,且OA=OC=1,则下列关系中正确的是( )| A. | a+b=-1 | B. | ac<0 | C. | b<2a | D. | a-b=-1 |
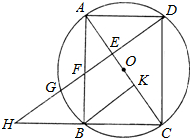 如图,已知:矩形ABCD,以对角线AC的中点O为圆心,OA的长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为点K,过点D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.
如图,已知:矩形ABCD,以对角线AC的中点O为圆心,OA的长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为点K,过点D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.
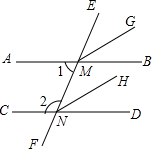 如图,直线EF分别交AB、CD于点M、N,MG平分∠EMB,NH平分∠END,并且MG∥NH,请说明∠1+∠2=180°的理由.
如图,直线EF分别交AB、CD于点M、N,MG平分∠EMB,NH平分∠END,并且MG∥NH,请说明∠1+∠2=180°的理由.