题目内容
5.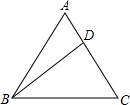 如图,在△ABC中,AB=AC=10,BC=12,有一点D在AC上移动,则AD+BD+CD的最小值是( )
如图,在△ABC中,AB=AC=10,BC=12,有一点D在AC上移动,则AD+BD+CD的最小值是( )| A. | 18 | B. | 18.6 | C. | 20 | D. | 19.6 |
分析 过点B作BD⊥AC,垂足为D.利用勾股定理求得AD=2.8,然后利用勾股定理求得BD的长,由垂线段最短可知:当BD⊥AC时,BD有最小值.
解答 解:过点B作BD⊥AC,垂足为D.
设AD=x,则DC=10-x.
在△ABD和△BCD中,由勾股定理得:AB2-AD2=BD2,BC2-DC2=DB2,
∴AB2-AD2=BC2-DC2,即102-x2=122-(10-x)2.
解得:x=2.8.
∴BD=$\sqrt{1{0}^{2}-2.{8}^{2}}$=9.6.
由垂线段最短可知:当BD⊥AC时,BD有最小值.
∴AD+BD+CD=BD+AC=9.6+10=19.6.
故选:D.
点评 本题主要考查的是垂线段的性质、勾股定理的应用,明确当BD⊥AC时,BD有最小值是解题的关键.

练习册系列答案
相关题目
13.若二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个不同的交点,坐标分别为(x1,0),(x2,0),且x1<x2,图象上有一点M (x0,y0)在x轴下方,则下列判断正确的是( )
| A. | a>0 | B. | a(x0-x1)( x0-x2)<0 | C. | x1<x0<x2 | D. | b2-4ac≥0 |
17.下列各题运算正确的是( )
| A. | 3a+3b=6ab | B. | a+a=a2 | C. | 16a2-9a2=7 | D. | 9ab-9ba=0 |
15.若等腰三角形中相等的两边的长为10cm,第三边长为16cm,则第三边的高为( )
| A. | 12cm | B. | 10cm | C. | 8cm | D. | 6cm |
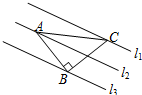 如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3,上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC的长是$\sqrt{68}$.
如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3,上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC的长是$\sqrt{68}$.
 如图,AB是半圆的直径,∠BAC=20°,D是$\widehat{AC}$的中点,则∠DAC的度数是35°.
如图,AB是半圆的直径,∠BAC=20°,D是$\widehat{AC}$的中点,则∠DAC的度数是35°.