题目内容
1.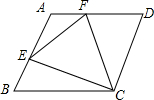 如图,在菱形ABCD中,∠B=60°,点E、F分别在边AB、AD上,且AE=DF.
如图,在菱形ABCD中,∠B=60°,点E、F分别在边AB、AD上,且AE=DF.(1)试判断△ECF的形状并说明理由;
(2)若AB=6,那么△ECF的周长是否存在最小值?如果存在,请求出来;如果不存在,请简要说明理由.
分析 (1)要判断△ECF的形状,只要得到各边的关系或者各角的关系即可,根据在菱形ABCD中,∠B=60°,点E、F分别在边AB、AD上,且AE=DF,可以得到三角形CEF各边的关系,从而可以解答本题;
(2)由题意可得,当边CE最短时,则△CEF的周长最短,根据点C到线段AB的最短距离是CE⊥AB,可以得到CE的长,本题得以解决.
解答 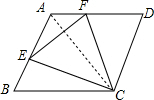 解:(1)△ECF是等边三角形,
解:(1)△ECF是等边三角形,
理由:连接CA,如右图所示,
∵四边形ABCD是菱形,∠B=60°,AE=DF,
∴AB=BC=CD=DA,∠BAD=120°,
∴∠FAC=60°,BE=AF,AB=BC=AC,
在△AFC和△BEC中,
$\left\{\begin{array}{l}{AF=BE}\\{∠FAC=∠B}\\{AC=BC}\end{array}\right.$,
∴△AFC≌△BEC(SAS)
∴CF=CE,∠ACF=∠BCE,
又∵∠BCE+∠ECA=60°,
∴∠ECA+∠ACF=60°,
∴△ECF是等边三角形;
(2)若AB=6,那么△ECF的周长存在最小值,最小值是3$\sqrt{3}$;
理由:∵∠B=60°,AB=2,点C到线段AB的最短距离是当线段CE⊥AB时,
∴∠BEC=90°,
∴CE=$\sqrt{3}$,
由(1)知△CEF是等边三角形,
∴△ECF的周长的最小值是$3\sqrt{3}$
点评 本题考查菱形的性质、最短路线问题,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
11.关于x的一元二次方程(a-1)x2-2x+3=0没有实数根,则整数a的最小值是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
10.有一箱子装有3张分别标示4,5,6的号码牌,已知小明以每次取一张且取后不放回的方式,先后取出2张牌,组成一个二位数,则组成的二位数是6的倍数的概率是( )
| A. | $\frac{7}{12}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
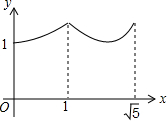
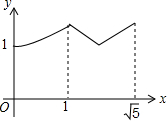
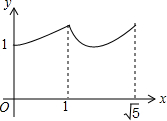
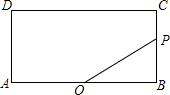 如图,矩形ABCD中,AB=2,BC=1,O是AB的中点,动点P从B点开始沿着边BC,CD运动到点D结束.设BP=x,OP=y,则y关于x的函数图象大致为( )
如图,矩形ABCD中,AB=2,BC=1,O是AB的中点,动点P从B点开始沿着边BC,CD运动到点D结束.设BP=x,OP=y,则y关于x的函数图象大致为( )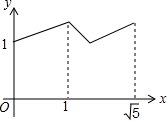
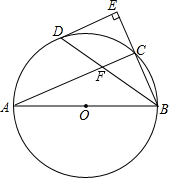 如图,已知AB为⊙O的直径,C为⊙O上异于A、B的一个动点,作∠ABC的平分线交⊙O于点D,过点D作⊙O的切线与BC的延长线交于点E,连接BD交AC于点F,小明经操作发现如下2个结论:①∠E为直角;②FA=FB,请你分别判断这两个结论是否成立?若成立,请给予证明;若不成立,请补充条件,使之成立.
如图,已知AB为⊙O的直径,C为⊙O上异于A、B的一个动点,作∠ABC的平分线交⊙O于点D,过点D作⊙O的切线与BC的延长线交于点E,连接BD交AC于点F,小明经操作发现如下2个结论:①∠E为直角;②FA=FB,请你分别判断这两个结论是否成立?若成立,请给予证明;若不成立,请补充条件,使之成立.