题目内容
18.学校准备购进一批排球和篮球,已知1个排球和2个篮球共需320元,3个排球和1个篮球共需360元.(1)求一个排球和一个篮球的售价各是多少元?
(2)学校准备购进这种排球和篮球共40个,且篮球的数量不少于排球数量的3倍,求最省钱的购买方案.
分析 (1)设一个排球的售价为x元,一个篮球的售价为y元,根据总价=单价×购买数量,即可得出关于x、y的二元一次方程,解之即可得出结论;
(2)设购买排球z个,所花费用为w元,则购买篮球(40-z)个,根据总价=单价×购买数量,即可得出w关于z的函数关系式,再根据篮球的数量不少于排球数量的3倍,可求出x的取值范围,利用一次函数的性质即可解决最值问题.
解答 解:(1)设一个排球的售价为x元,一个篮球的售价为y元,
根据题意得:$\left\{\begin{array}{l}{x+2y=320}\\{3x+y=360}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=80}\\{y=120}\end{array}\right.$.
答:一个排球的售价为80元,一个篮球的售价为120元.
(2)设购买排球z个,所花费用为w元,则购买篮球(40-z)个,
根据题意得:w=80z+120(40-z)=-40x+4800.
又∵40-x≥3x,
∴x≤10.
∵k=-40<0,
∴当x=10时,w最小.
∴最省钱的购买方案为:购买排球10个,篮球30个.
点评 本题考查了一次函数的应用、二元一次方程组的应用以及解一元一次不等式,解题的关键是:(1)根据总价=单价×购买数量,列出关于x、y的二元一次方程;(2)根据总价=单价×购买数量,找出w关于z的函数关系式.

练习册系列答案
相关题目
7.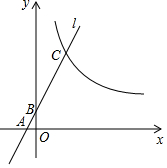 如图,直线l分别交x轴、y轴于点A、B,交双曲线y=$\frac{k}{x}$(x>0)于点C,若AB:AC=1:3,且S△AOB=$\frac{\sqrt{3}}{8}$,则k的值为( )
如图,直线l分别交x轴、y轴于点A、B,交双曲线y=$\frac{k}{x}$(x>0)于点C,若AB:AC=1:3,且S△AOB=$\frac{\sqrt{3}}{8}$,则k的值为( )
 如图,直线l分别交x轴、y轴于点A、B,交双曲线y=$\frac{k}{x}$(x>0)于点C,若AB:AC=1:3,且S△AOB=$\frac{\sqrt{3}}{8}$,则k的值为( )
如图,直线l分别交x轴、y轴于点A、B,交双曲线y=$\frac{k}{x}$(x>0)于点C,若AB:AC=1:3,且S△AOB=$\frac{\sqrt{3}}{8}$,则k的值为( )| A. | $\frac{3\sqrt{3}}{2}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
 一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后分别按原速同时驶往甲地,两车之间的距离S(km)与慢车行驶时间t(h)之间的函数图象如图所示,则快车到达甲地时,慢车距离甲地60km.
一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后分别按原速同时驶往甲地,两车之间的距离S(km)与慢车行驶时间t(h)之间的函数图象如图所示,则快车到达甲地时,慢车距离甲地60km. 如图,一艘轮船在A处时观测得小岛C在船的北偏东60°方向,轮船以40海里/时的速度向正东方向航行1.5小时到达B处,这时小岛C在船的北偏东30°方向.已知小岛C周围50海里范围内是暗礁区.
如图,一艘轮船在A处时观测得小岛C在船的北偏东60°方向,轮船以40海里/时的速度向正东方向航行1.5小时到达B处,这时小岛C在船的北偏东30°方向.已知小岛C周围50海里范围内是暗礁区. 图是由5个大小相同的小正方体摆成的立体图形,它的俯视图是( )
图是由5个大小相同的小正方体摆成的立体图形,它的俯视图是( )


