题目内容
13．化简：（1）$\frac{{a}^{2}+2ab+{b}^{2}}{2ab}$÷（a+b）2；
（2）$\frac{x}{{x}^{2}-4}$-$\frac{1}{2x-4}$．
分析 （1）根据分式的除法可以解答本题；
（2）根据分式的减法可以解答本题．
解答 解：（1）$\frac{{a}^{2}+2ab+{b}^{2}}{2ab}$÷（a+b）2
=$\frac{（a+b）^{2}}{2ab}•\frac{1}{（a+b）^{2}}$
=$\frac{1}{2ab}$；
（2）$\frac{x}{{x}^{2}-4}$-$\frac{1}{2x-4}$
=$\frac{x}{（x+2）（x-2）}-\frac{1}{2（x-2）}$
=$\frac{2x-（x+2）}{2（x+2）（x-2）}$
=$\frac{x-2}{2（x+2）（x-2）}$
=$\frac{1}{2（x+2）}$
=$\frac{1}{2x+4}$．
点评 本题考查分式的混合运算，解答本题的关键是明确分式混合的计算方法．
练习册系列答案
天天练口算系列答案
相关题目
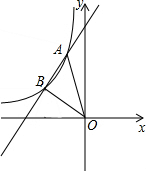一次函数y=x+5的图象与反比例函数y=$\frac{k}{x}$（k＜0）在第二象限的图象交于A（-1，n）和B两点．
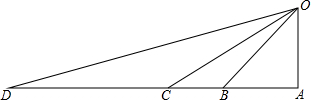政府为开发“江心岛O”，从仓储D处调集物资，计划先用汽车运到与D在同一直线上的C，B，A三个码头中的一处，再用货船运到小岛O．已知：OA⊥AD，∠ODA=15°，∠OCA=30°，∠OBA=45°，CD=20km．若汽车行驶的速度为50km/时，货船航行的速度为25km/时，