题目内容
14．关于多项式-2x2+8x+5的说法正确的是（ ）| A． | 有最大值13 | B． | 有最小值-3 | C． | 有最大值37 | D． | 有最小值1 |
分析 利用配方法将已知多项式转化为-2（x-2）2+13的形式，然后利用非负数的性质进行解答．
解答 解：-2x2+8x+5=-2（x-2）2+13，
∵（x-2）2≥0，
∴-2（x-2）2+13≤13，即多项式-2x2+8x+5的最大值为13，没有最小值．
故选：A．
点评 本题考查了非负数的性质和配方法的应用．解题时要注意配方法的步骤．注意在变形的过程中不要改变式子的值．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
已知：如图，在△ABC中，∠ABC=∠ACB，AD⊥BD，AE⊥CE，且AD=AE．求证：△AEC≌△ADB．
已知：△ABC中，∠A=90°，点O是正方形BCDE对角线的交点．求证：AO是∠A的角平分线．
作图题：（要求：在下列空白处尺规作图，保留作图痕迹，不写作法，要作答．）
如图所示，E，F分别是矩形ABCD的边BC，CD上的点，用S△CEF表示△CEF的面积，若S△CEF=3，S△ABE=4，S△ADF=5，则S△AEF=8．
4．
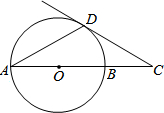如图，AB是⊙O直径，C是AB延长线上一点，CD是⊙O的切线，D为切点，∠A=30°，AB=2cm，则CD的长为（ ）
如图，AB是⊙O直径，C是AB延长线上一点，CD是⊙O的切线，D为切点，∠A=30°，AB=2cm，则CD的长为（ ）| A． | 2cm | B． | $\frac{3}{2}$cm | C． | $\sqrt{3}$cm | D． | $\frac{\sqrt{3}}{2}$cm |