题目内容
4.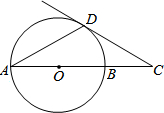 如图,AB是⊙O直径,C是AB延长线上一点,CD是⊙O的切线,D为切点,∠A=30°,AB=2cm,则CD的长为( )
如图,AB是⊙O直径,C是AB延长线上一点,CD是⊙O的切线,D为切点,∠A=30°,AB=2cm,则CD的长为( )| A. | 2cm | B. | $\frac{3}{2}$cm | C. | $\sqrt{3}$cm | D. | $\frac{\sqrt{3}}{2}$cm |
分析 连接OD,根据等边对等角以及三角形的外角的性质求得∠DOB的度数,然后在直角△ODC中利用三角函数求解.
解答  解:连接OD.
解:连接OD.
∵OA=OD,
∴∠A=∠ADO=30°,
∴∠DOC=60°,
∵CD是⊙O的切线,D为切点,
∴∠ODC=90°,
∴∠C=90°-∠DOC=90°-60°=30°.
又∵OD=$\frac{1}{2}$AB=1cm.
∴CD=$\sqrt{3}$cm.
故选C.
点评 本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
14.关于多项式-2x2+8x+5的说法正确的是( )
| A. | 有最大值13 | B. | 有最小值-3 | C. | 有最大值37 | D. | 有最小值1 |
15.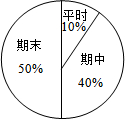 小军和小明八年级上学期的数学成绩如下表所示:
小军和小明八年级上学期的数学成绩如下表所示:
(1)计算小军和小明上学期平时的平均成绩;
(2)如果总评成绩按扇形图所示的权重计算,问小军和小明谁的上学期总评成绩高?
 小军和小明八年级上学期的数学成绩如下表所示:
小军和小明八年级上学期的数学成绩如下表所示:| 测验 类别 | 平 时 | 期中 考试 | 期末 考试 | |||
| 测验1 | 测验2 | 测验3 | 测验4 | |||
| 小军成绩 | 110 | 105 | 95 | 110 | 108 | 112 |
| 小明成绩 | 105 | 95 | 100 | 115 | 115 | 95 |
(2)如果总评成绩按扇形图所示的权重计算,问小军和小明谁的上学期总评成绩高?
9.下列约分正确的是( )
| A. | $\frac{x+y}{{x}^{2}+xy}$=$\frac{1}{x}$ | B. | $\frac{{x}^{6}}{{x}^{2}}$=x3 | C. | $\frac{x+y}{x+y}=0$ | D. | $\frac{2x{y}^{2}}{4{x}^{2}y}$=$\frac{1}{2}$ |
 如图,点P是正方形ABCD对角线BD上的一点,PM⊥BC,PN⊥DC,垂足分别为M、N.
如图,点P是正方形ABCD对角线BD上的一点,PM⊥BC,PN⊥DC,垂足分别为M、N.