题目内容
5. 已知:如图,在△ABC中,∠ABC=∠ACB,AD⊥BD,AE⊥CE,且AD=AE.求证:△AEC≌△ADB.
已知:如图,在△ABC中,∠ABC=∠ACB,AD⊥BD,AE⊥CE,且AD=AE.求证:△AEC≌△ADB.
分析 由等腰三角形的判定定理得出AB=AC,由HL证明Rt△AEC≌Rt△ADB即可.
解答 证明:∵∠ABC=∠ACB,
∴AB=AC,
∵AD⊥BD,AE⊥CE,
∴∠D=∠E=90°,
即△AEC和△ADB是直角三角形,
在Rt△AEC和Rt△ADB中,$\left\{\begin{array}{l}{AC=AB}\\{AE=AD}\end{array}\right.$,
∴Rt△AEC≌Rt△ADB(HL).
点评 本题考查了等腰三角形的判定定理、直角三角形全等的判定方法;熟练掌握全等三角形的判定方法,证明三角形是等腰三角形是解决问题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
16.下列各组数是勾股数的是( )
| A. | 2,3,4 | B. | 4,5,6 | C. | 3.6,4,8.6 | D. | 9,40,41 |
13.下列事件为必然事件的是( )
| A. | 任意买一张电影票,座位号是偶数 | |
| B. | 打开电视机,CCTV第一套节目正在播放天气预报 | |
| C. | 从一个之装有红色小球的把它们袋中,任意摸出一球是红球 | |
| D. | 经过某一有交通信号灯的路口,恰好遇到红灯 |
17.已知关于x方程2x2-x+3=0,下列叙述正确的是( )
| A. | 有一个实数根 | B. | 有两个不相等的实数根 | ||
| C. | 有两个相等的实数根 | D. | 无实数根 |
14.关于多项式-2x2+8x+5的说法正确的是( )
| A. | 有最大值13 | B. | 有最小值-3 | C. | 有最大值37 | D. | 有最小值1 |
15. 小军和小明八年级上学期的数学成绩如下表所示:
小军和小明八年级上学期的数学成绩如下表所示:
(1)计算小军和小明上学期平时的平均成绩;
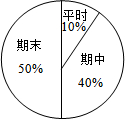
(2)如果总评成绩按扇形图所示的权重计算,问小军和小明谁的上学期总评成绩高?
 小军和小明八年级上学期的数学成绩如下表所示:
小军和小明八年级上学期的数学成绩如下表所示:| 测验 类别 | 平 时 | 期中 考试 | 期末 考试 | |||
| 测验1 | 测验2 | 测验3 | 测验4 | |||
| 小军成绩 | 110 | 105 | 95 | 110 | 108 | 112 |
| 小明成绩 | 105 | 95 | 100 | 115 | 115 | 95 |
(2)如果总评成绩按扇形图所示的权重计算,问小军和小明谁的上学期总评成绩高?
 如图,△ABC中,DE是BC的垂直平分线.若AC=8cm,△ABE的周长为14cm,则AB的长为6cm.
如图,△ABC中,DE是BC的垂直平分线.若AC=8cm,△ABE的周长为14cm,则AB的长为6cm. 如图,∠B=80°,∠C=50°,AD是△ABC的高,AE是∠CAB的平分线,求∠DAE.
如图,∠B=80°,∠C=50°,AD是△ABC的高,AE是∠CAB的平分线,求∠DAE.