题目内容
9. 已知:△ABC中,∠A=90°,点O是正方形BCDE对角线的交点.求证:AO是∠A的角平分线.
已知:△ABC中,∠A=90°,点O是正方形BCDE对角线的交点.求证:AO是∠A的角平分线.
分析 根据正方形的性质得出∠OCB=∠OBC=45°,∠COB=∠BAC=90°,∠BAC+∠COB=180°,推出A、C、O、B四点共圆,根据圆周角定理得出∠CAO=∠OBC=45°,∠BAO=∠OCB=45°,即可得出答案.
解答 证明:∵四边形BCDE是正方形,
∴∠OCB=∠OBC=45°,∠COB=∠BAC=90°,
∴∠BAC+∠COB=180°,
∴A、C、O、B四点共圆,
∴∠CAO=∠OBC=45°,∠BAO=∠OCB=45°,
∴∠BAO=∠CAO,
∴AO是∠A的角平分线.
点评 本题考查了角平分线性质,圆内角三角形的性质,圆周角定理,正方形的性质的应用,解此题的关键是推出A、C、O、B四点共圆,难度适中.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
17.已知关于x方程2x2-x+3=0,下列叙述正确的是( )
| A. | 有一个实数根 | B. | 有两个不相等的实数根 | ||
| C. | 有两个相等的实数根 | D. | 无实数根 |
14.关于多项式-2x2+8x+5的说法正确的是( )
| A. | 有最大值13 | B. | 有最小值-3 | C. | 有最大值37 | D. | 有最小值1 |
18.分式方程$\frac{2x-7}{x-2}$=1的解是( )
| A. | x=2 | B. | x=5 | C. | x=-1 | D. | x=1 |
 如图,△ABC中,DE是BC的垂直平分线.若AC=8cm,△ABE的周长为14cm,则AB的长为6cm.
如图,△ABC中,DE是BC的垂直平分线.若AC=8cm,△ABE的周长为14cm,则AB的长为6cm.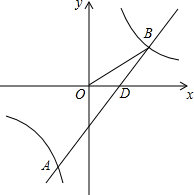 如图,已知A(n,-4),B(3,2)是一次函数y1=kx+b的图象和反比例函数y2=$\frac{m}{x}$的图象的两个交点,直线AB与x轴交于点D.
如图,已知A(n,-4),B(3,2)是一次函数y1=kx+b的图象和反比例函数y2=$\frac{m}{x}$的图象的两个交点,直线AB与x轴交于点D.