题目内容
3.如图,一次函数与反比例函数y=$\frac{4}{x}$的图象在第一象限交于A、B两点,且交x轴于点C,交y轴于点F,若$\frac{CB}{CA}$=$\frac{1}{3}$,连接OA交反比例函数y=$\frac{k}{x}$(k>0)的图象于点D,连接BD,若S△ADB=$\frac{8}{3}$,则k的值为1.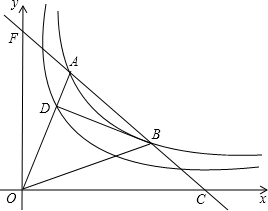
分析 作AM⊥OC于M,BN⊥OC于N,根据已知得出$\frac{BN}{AM}$=$\frac{CB}{CA}$=$\frac{1}{3}$,设B(m,$\frac{4}{m}$),则A($\frac{m}{3}$,$\frac{12}{m}$),根据反比例系数k的几何意义可知S△AOB=S梯形AMNB=$\frac{16}{3}$,从而求得AD=OD,得出D($\frac{m}{6}$,$\frac{6}{m}$),代入y=$\frac{k}{x}$(k>0)即可求得k的值.
解答 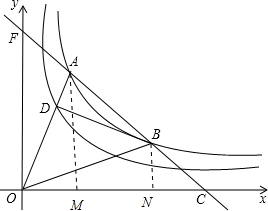 解:作AM⊥OC于M,BN⊥OC于N,
解:作AM⊥OC于M,BN⊥OC于N,
∵S△AOM=S△BON=$\frac{1}{2}$×4=2,
∴S△AOB=S梯形AMNB,
设B(m,$\frac{4}{m}$),
∵AM∥BN,$\frac{CB}{CA}$=$\frac{1}{3}$,
∴$\frac{BN}{AM}$=$\frac{CB}{CA}$=$\frac{1}{3}$,
∴A($\frac{m}{3}$,$\frac{12}{m}$),
∴S△AOB=$\frac{1}{2}$($\frac{4}{m}$+$\frac{12}{m}$)×(m-$\frac{m}{3}$)=$\frac{16}{3}$,
∵S△ADB=$\frac{8}{3}$,
∴S△BOD=$\frac{8}{3}$,
∴AD=OD,
∴D($\frac{m}{6}$,$\frac{6}{m}$),
∵D在反比例函数y=$\frac{k}{x}$(k>0)的图象上,
∴k=$\frac{m}{6}$×$\frac{6}{m}$=1.
故答案为1.
点评 本题考查了反比例函数和一次函数的交点,反比例函数系数k的几何意义,根据反比例函数系数k的几何意义得出S△AOB=S梯形AMNB是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 4:1 | B. | 1:2 | C. | 2:1 | D. | 1:4 |
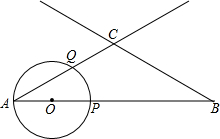 如图,AB=3,∠A=∠B=30°,动点O从A出发,沿AB方向以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤1.5).以O为圆心,OA长为半径的⊙O与射线AB,AC的另一个交点分别为P,Q,连接CP,PQ.
如图,AB=3,∠A=∠B=30°,动点O从A出发,沿AB方向以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤1.5).以O为圆心,OA长为半径的⊙O与射线AB,AC的另一个交点分别为P,Q,连接CP,PQ.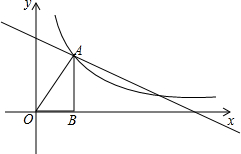 如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于A、C两点,点C坐标是(6,1),AB⊥x轴于点B,且AB=3.
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于A、C两点,点C坐标是(6,1),AB⊥x轴于点B,且AB=3. 如图,△ABD、△ADE、△AEC都是顶角为30°的等腰三角形,∠AEF=15°,AF=1,则BD=$\sqrt{2}$.
如图,△ABD、△ADE、△AEC都是顶角为30°的等腰三角形,∠AEF=15°,AF=1,则BD=$\sqrt{2}$. 如图所示,在?ABCD中,AB=2BC,点M是DC的中点,BE⊥AD,E是垂足,求证:∠EMC=3∠DEM.
如图所示,在?ABCD中,AB=2BC,点M是DC的中点,BE⊥AD,E是垂足,求证:∠EMC=3∠DEM.