题目内容
12. 如图所示,在?ABCD中,AB=2BC,点M是DC的中点,BE⊥AD,E是垂足,求证:∠EMC=3∠DEM.
如图所示,在?ABCD中,AB=2BC,点M是DC的中点,BE⊥AD,E是垂足,求证:∠EMC=3∠DEM.
分析 延长EM交BC的延长线于F,连接BM,根据已知条件证得△DEM≌△CFM,得到EM=FM,由于AD∥BC,BE⊥AD,于是得到△EBF是直角三角形,BM为斜边的中线,得到MF=BM,推出∠F=∠MBC,根据已知条件AB=2BC,AB=CD=$\frac{1}{2}$CM,得到∠MBC=∠CMB,根据外角的性质得到∠MCF=∠MBC+∠CMB=2∠F.于是得到∠EMC=∠F+∠MCF=3∠F=3∠DEM.
解答  证明:延长EM交BC的延长线于F,连接BM,
证明:延长EM交BC的延长线于F,连接BM,
在?ABCD中,
∵AD∥BC,
∴∠DEM=∠F,
在△DEM与△CFM中,
$\left\{\begin{array}{l}{∠DME=∠CMF}\\{∠DEM=∠F}\\{DM=CM}\end{array}\right.$,
∴△DEM≌△CFM,
∴EM=FM,
∵AD∥BC,BE⊥AD,
∴BE⊥BC,
∴△EBF是直角三角形,BM为斜边的中线,
∴MF=BM,
∴∠F=∠MBC,
∵AB=2BC,AB=CD=$\frac{1}{2}$CM,
∴∠MBC=∠CMB,
则∠MCF=∠MBC+∠CMB=2∠F.
∴∠EMC=∠F+∠MCF=3∠F=3∠DEM.
点评 本题主要考查了平行四边形的性质,全等三角形的判定及性质以及直角三角形斜边中线问题,正确的做出辅助线是解题的关键.

练习册系列答案
相关题目
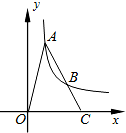 如图,A、B是双曲线y=$\frac{k}{x}$(k>0)上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=6.则k=( )
如图,A、B是双曲线y=$\frac{k}{x}$(k>0)上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=6.则k=( )