Question

12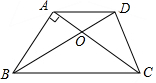．如图，已知梯形ABCD中，AD?BC，AC、BD相交于点O，AB⊥AC，AD=CD，AB=3，BC=5．求：
（1）tan∠ACD的值；
（2）梯形ABCD的面积．

Answer 1

分析 （1）作DE∥AB交BC于E，交AC于M，证出DE⊥AC，由等腰三角形的性质得出AM=CM，证明四边形ABED是平行四边形，得出DE=AB=3，在Rt△ABC中，由勾股定理求出AC=4，得出AM=CM=2，由平行线分线段成比例定理得出DM=EM=$\frac{1}{2}$DE=$\frac{3}{2}$，即可求出tan∠ACD=$\frac{DM}{CM}$=$\frac{3}{4}$；
（2）梯形ABCD的面积=△ABC的面积+△ACD的面积，即可得出答案．

解答 解：（1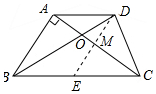）作DE∥AB交BC于E，交AC于M，如图所示：
∵AB⊥AC，DE∥AB，
∴DE⊥AC，
∵AD=CD，
∴AM=CM，
∵AD∥BC，DE∥AB，
∴四边形ABED是平行四边形，
∴DE=AB=3，
在Rt△ABC中，AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4，
∴AM=CM=2，
∵AD∥BC，
∴DM：EM=AM：CM=1：1，
∴DM=EM=$\frac{1}{2}$DE=$\frac{3}{2}$，
∴tan∠ACD=$\frac{DM}{CM}$=$\frac{\frac{3}{2}}{2}$=$\frac{3}{4}$；

（2）梯形ABCD的面积=△ABC的面积+△ACD的面积=$\frac{1}{2}$×3×4+$\frac{1}{2}$×4×$\frac{3}{2}$=9．

点评 本题考查了梯形的性质、等腰三角形的性质、勾股定理、平行线的性质、平行线分线段成比例定理、梯形和三角形面积的计算等知识；本题综合性强，有一定难度．