题目内容
(1)解方程:
x(x-1)-(x-1)=0.
(2)已知抛物线y=-2x2+8x-6,请用配方法把它化成y=a(x-h)2+k的形式,并指出此抛物线的顶点坐标和对称轴.
| 1 |
| 2 |
(2)已知抛物线y=-2x2+8x-6,请用配方法把它化成y=a(x-h)2+k的形式,并指出此抛物线的顶点坐标和对称轴.
考点:二次函数的三种形式,解一元二次方程-因式分解法
专题:
分析:(1)先将把方程左边化为两个一次因式积的形式,然后根据两数相乘积为0,两因式至少有一个为0转化为两个一元一次方程,求出方程的解即可得到原方程的解;
(2)先利用配方法提出二次项系数,加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式,再根据二次函数的性质即可写出抛物线的对称轴和顶点坐标.
(2)先利用配方法提出二次项系数,加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式,再根据二次函数的性质即可写出抛物线的对称轴和顶点坐标.
解答:解:(1)
x(x-1)-(x-1)=0,
分解因式得:(x-1)(
x-1)=0,
可化为:x-1=0或
x-1=0,
解得:x1=1,x2=2;
(2)∵y=-2x2+8x-6=-2(x2-4x+4)+8-6=-2(x-2)2+2,
∴此抛物线的顶点坐标是(2,2),对称轴为直线x=2.
| 1 |
| 2 |
分解因式得:(x-1)(
| 1 |
| 2 |
可化为:x-1=0或
| 1 |
| 2 |
解得:x1=1,x2=2;
(2)∵y=-2x2+8x-6=-2(x2-4x+4)+8-6=-2(x-2)2+2,
∴此抛物线的顶点坐标是(2,2),对称轴为直线x=2.
点评:本题考查了二次函数解析式的三种形式,二次函数的性质及解一元二次方程-因式分解法,难度适中.

练习册系列答案
相关题目
 如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )
如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )| A、2 | ||
| B、4 | ||
C、
| ||
D、
|
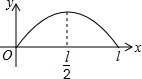 点P从点O出发,按逆时针方向沿周长为l的图形运动一周,O,P两点间的距离y与点P走过的路程x的函数关系如图,那么点P所走的图形是( )
点P从点O出发,按逆时针方向沿周长为l的图形运动一周,O,P两点间的距离y与点P走过的路程x的函数关系如图,那么点P所走的图形是( )


 1883年,德国数学家格奥尔格•康托尔引入位于一条线段上的一些点的集合,它的做法如下:
1883年,德国数学家格奥尔格•康托尔引入位于一条线段上的一些点的集合,它的做法如下: