题目内容
 1883年,德国数学家格奥尔格•康托尔引入位于一条线段上的一些点的集合,它的做法如下:
1883年,德国数学家格奥尔格•康托尔引入位于一条线段上的一些点的集合,它的做法如下:取一条长度为1的线段,将它三等分,去掉中间一段,余下两条线段,达到第1阶段;将剩下的两条线段再分别三等分,各去掉中间一段,余下四条线段,达到第2阶段;再将剩四条线段,分别三等分,分别去掉中间一段,余下八条线段,达到第3阶段;…;这样的操作一直继续下去,在不断分割舍弃过程中,所形成的线段数目越来越多,把这种分形,称作康托尔点集,如图是康托尔点集的最初几个阶段,当达到第5个阶段时,余下的线段的长度之和为
考点:规律型:图形的变化类
专题:
分析:根据题意具体表示出前几个式子,然后推而广之发现规律.
解答:解:根据题意知:第一阶段时,余下的线段的长度之和为
,
第二阶段时,余下的线段的长度之和为
×
=(
)2,
第三阶段时,余下的线段的长度之和为
×
×
=(
)3,
…
以此类推,
第五个阶段时,余下的线段的长度之和为(
)5,
当达到第n个阶段时(n为正整数),余下的线段的长度之和为(
)n.
故答案为:(
)5;(
)n.
| 2 |
| 3 |
第二阶段时,余下的线段的长度之和为
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
第三阶段时,余下的线段的长度之和为
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
…
以此类推,
第五个阶段时,余下的线段的长度之和为(
| 2 |
| 3 |
当达到第n个阶段时(n为正整数),余下的线段的长度之和为(
| 2 |
| 3 |
故答案为:(
| 2 |
| 3 |
| 2 |
| 3 |
点评:此题考查图形的变化规律,找出图形之间的联系,得出规律,解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列事件是随机事件的是( )
| A、明天太阳从东方升起 |
| B、任意画一个三角形,其内角和是360° |
| C、通常温度降到0℃以下,纯净的水结冰 |
| D、射击运动员射击一次,命中靶心 |
若3a=2b,则
的值为( )
| a-b |
| a |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
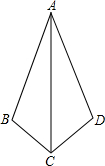 如图,∠BAC=∠DAC,∠B=∠D.求证:AB=AD.
如图,∠BAC=∠DAC,∠B=∠D.求证:AB=AD.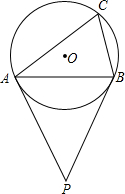 如图,已知PA、PB分别切⊙O于A、B,点C在⊙O上,∠BCA=75°,则∠P=
如图,已知PA、PB分别切⊙O于A、B,点C在⊙O上,∠BCA=75°,则∠P=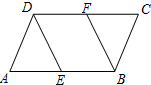 如图,在平行四边形ABCD中,AE=CF.求证:
如图,在平行四边形ABCD中,AE=CF.求证: