题目内容
15.抛物线y=x2+x+2上三点(-2,a)、(-1,b),(3,c),则a、b、c的大小关系是c>a>b.分析 先根据二次函数的性质得到抛物线的对称轴为直线x=-$\frac{1}{2}$,然后比较三个点都直线x=-$\frac{1}{2}$的远近得到a、b、c的大小关系.
解答 解:∵二次函数的解析式为y=x2+x+2=(x+$\frac{1}{2}$)2+$\frac{7}{4}$,
∴抛物线的对称轴为直线x=-$\frac{1}{2}$,
∵(-2,a)、(-1,b),(3,c),
∴点(3,c)离直线x=-$\frac{1}{2}$最远,(-1,b)离真相x=-$\frac{1}{2}$最近,
而抛物线开口向上,
∴c>a>b;
故答案为c>a>b.
点评 题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
18.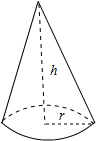 如图,圆锥体的高h=2$\sqrt{3}$cm,底面圆半径r=2cm,则圆锥体的全面积为( )
如图,圆锥体的高h=2$\sqrt{3}$cm,底面圆半径r=2cm,则圆锥体的全面积为( )
 如图,圆锥体的高h=2$\sqrt{3}$cm,底面圆半径r=2cm,则圆锥体的全面积为( )
如图,圆锥体的高h=2$\sqrt{3}$cm,底面圆半径r=2cm,则圆锥体的全面积为( )| A. | 4$\sqrt{3}$πcm2 | B. | 8πcm2 | C. | 12πcm2 | D. | (4$\sqrt{3}$+4)πcm2 |
20.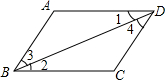 如图,下列推理中,正确个数是( )
如图,下列推理中,正确个数是( )
(1)∵AB∥CD,∴∠ABC+∠C=180°
(2)∵∠1=∠2,∴AD∥BC
(3)∵AD∥BC,∴∠3=∠4
(4)∵∠A+∠ADC=180°,∴AB∥CD.
 如图,下列推理中,正确个数是( )
如图,下列推理中,正确个数是( )(1)∵AB∥CD,∴∠ABC+∠C=180°
(2)∵∠1=∠2,∴AD∥BC
(3)∵AD∥BC,∴∠3=∠4
(4)∵∠A+∠ADC=180°,∴AB∥CD.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.三角形的两边长为6和10,要使这个三角形为直角三角形,则第三边长为( )
| A. | 8 | B. | 9 | C. | 2$\sqrt{34}$或8 | D. | 2$\sqrt{34}$或9 |