题目内容
12.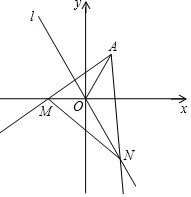 如图,点A(1,$\sqrt{3}$),直线l:y=-$\sqrt{3}$x,射线AM、AN分别交x轴负半轴,直线l于点M,N,∠MAN=60°,则△OMN的面积为$\sqrt{3}$.
如图,点A(1,$\sqrt{3}$),直线l:y=-$\sqrt{3}$x,射线AM、AN分别交x轴负半轴,直线l于点M,N,∠MAN=60°,则△OMN的面积为$\sqrt{3}$.
分析 由点A的坐标特点和勾股定理得出OA=2,∠AOM=∠AON=120°,由已知条件得出∠ONA=∠OAM,即可得出△OAN∽OMA,得出OA:OM=ON:OA,设N(b,-$\sqrt{3}$b),M(-a,0),从而求得ab=2,然后根据三角形面积根式即可求得.
解答  解:∵点A的坐标为A(1,$\sqrt{3}$),
解:∵点A的坐标为A(1,$\sqrt{3}$),
∴OA=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2,∠1=60°,
∵直线l:y=-$\sqrt{3}$x,
∴∠2=60°,
∴∠AOM=∠AON=120°,
∴∠OAN+∠ONA=60°,
∵∠MAN=60°,
∴∠ONA=∠OAM,
∴△OAN∽OMA,
∴OA:OM=ON:OA,
∴OA2=OM•ON,
设N(b,-$\sqrt{3}$b),M(-a,0),
∴ON=2b,OM=a,
∴a•2b=4,
∴ab=2,
∴S△MON=$\frac{1}{2}$•a•$\sqrt{3}$b=$\sqrt{3}$;
故答案为$\sqrt{3}$.
点评 本题是相似形综合题目,考查了勾股定理、解直角三角形、相似三角形的判定与性质、三角形面积等;本题综合性强,有一定难度,证明三角形相似是解决问题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
4.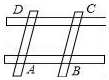 如图所示是由四根木棒搭成的平行四边形框架,AB=8cm,AD=6cm,在这个位置,将AB固定,逆时针转动AD.则关于?ABCD面积S的变化描述正确的是( )
如图所示是由四根木棒搭成的平行四边形框架,AB=8cm,AD=6cm,在这个位置,将AB固定,逆时针转动AD.则关于?ABCD面积S的变化描述正确的是( )
 如图所示是由四根木棒搭成的平行四边形框架,AB=8cm,AD=6cm,在这个位置,将AB固定,逆时针转动AD.则关于?ABCD面积S的变化描述正确的是( )
如图所示是由四根木棒搭成的平行四边形框架,AB=8cm,AD=6cm,在这个位置,将AB固定,逆时针转动AD.则关于?ABCD面积S的变化描述正确的是( )| A. | 保持不变 | B. | 先变小,再变大 | C. | 先变大,再变小 | D. | 0<S<48 |
 在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.
在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.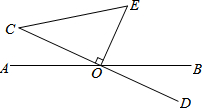 如图,AB,CD交于点O,OE⊥CD于O,连接CE,
如图,AB,CD交于点O,OE⊥CD于O,连接CE, 如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:①∠DCF=$\frac{1}{2}$∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.其中一定成立的是①②④.(把所有正确结论的序号都填在横线上)
如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:①∠DCF=$\frac{1}{2}$∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.其中一定成立的是①②④.(把所有正确结论的序号都填在横线上)