题目内容
 已知:关于x的一元二次方程mx2-(m+3)x+3=0有两个不相等的实数根.
已知:关于x的一元二次方程mx2-(m+3)x+3=0有两个不相等的实数根.(1)求m的取值范围;
(2)若m为正整数,设方程的两个整数根分别为p,q(p<q),求点P(p,q)的坐标;
(3)在(2)的条件下,分别在y轴和直线y=x上取点M、N,使△PMN的周长最小,求△PMN的周长.
考点:轴对称-最短路线问题,解一元二次方程-公式法,根的判别式
专题:
分析:(1)利用根的判别式列出不等式,然后求解即可;
(2)利用求根公式法表示出方程的两个根,再根据x是整数、m是正整数求出p、q,然后写出坐标即可;
(3)取点P关于y轴的对称点P′,点P关于直线y=x的对称点P″,根据轴对称确定最短路线问题,连接P′P″与y轴的交点即为点M,与直线y=x的交点即为点N,利用勾股定理列式求出P′P′,即为△PMN的周长最小值.
(2)利用求根公式法表示出方程的两个根,再根据x是整数、m是正整数求出p、q,然后写出坐标即可;
(3)取点P关于y轴的对称点P′,点P关于直线y=x的对称点P″,根据轴对称确定最短路线问题,连接P′P″与y轴的交点即为点M,与直线y=x的交点即为点N,利用勾股定理列式求出P′P′,即为△PMN的周长最小值.
解答:(1)解:∵关于x的一元二次方程mx2-(m+3)x+3=0有两个不相等的实数根,
∴△=[-(m+3)]2-4m×3=m2-6m+9=(m-3)2,m≠0,
∵△>0,
∴m≠3,
即m的取值范围为m≠0且m≠3;
(2)解:由求根公式,得x=
,
∴x1=1,x2=
,
∵m为正整数,方程根为整数,
∴m=1,m=3,
∵m≠3,
∴m=1,
∴x=2+1=3,
∵p<q,
∴p=1,q=3,
∴P(1,3);
(3)作点P关于y轴的对称点P′,
∴P′(-1,3),
作点P关于直线y=x的对称点P″,
∴P″(3,1),
连接P′P″,与y轴和直线y=x的交点分别是点M、N,
即△PMN的周长最小,
由勾股定理得,P′P″=
=2
,
即△PMN的周长最小值为2
.
∴△=[-(m+3)]2-4m×3=m2-6m+9=(m-3)2,m≠0,
∵△>0,
∴m≠3,
即m的取值范围为m≠0且m≠3;
(2)解:由求根公式,得x=
| (m+3)±(m-3) |
| 2m |
∴x1=1,x2=
| 3 |
| m |
∵m为正整数,方程根为整数,
∴m=1,m=3,
∵m≠3,
∴m=1,
∴x=2+1=3,
∵p<q,
∴p=1,q=3,

∴P(1,3);
(3)作点P关于y轴的对称点P′,
∴P′(-1,3),
作点P关于直线y=x的对称点P″,
∴P″(3,1),
连接P′P″,与y轴和直线y=x的交点分别是点M、N,
即△PMN的周长最小,
由勾股定理得,P′P″=
| [3-(-1)]2+(3-1)2 |
| 5 |
即△PMN的周长最小值为2
| 5 |
点评:本题考查了利用求根公式法解一元二次方程,根的判别式,利用轴对称确定最短路线问题,(2)判断出m的值是解题的关键,(3)难点在于确定出点M、N的位置.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
先作二次函数y=2x2+bx+c关于x轴对称的图象,再绕图象的顶点旋转180度,得到二次函数y=ax2-8x+5,则a、b、c的取值分别是( )
| A、2,-8,11 |
| B、2,-8,5 |
| C、-2,-8,11 |
| D、-2,-8,5 |
 如图,直线y=kx+1(k≠0)经过点A.
如图,直线y=kx+1(k≠0)经过点A.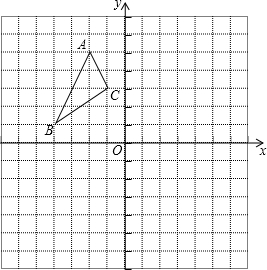 利用图中的网格线(最小的正方形的边长为1)画图:
利用图中的网格线(最小的正方形的边长为1)画图: 线段AB在平面直角坐标系中的位置如图所示,O为坐标原点.
线段AB在平面直角坐标系中的位置如图所示,O为坐标原点.