题目内容
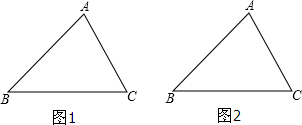
如图1,△ABC中,AB=AC,点D在BC上,点E、F分别在AD和AD的延长线上,且∠AEC=∠BAC,BF∥CE.
(1)求证:∠AFB与∠BAC互补;
(2)图1中是否存在与AF相等的线段?若存在,请找出,并加以证明,若不存在,说明理由.
(3)若将“AB=AC,点D在BC上,点E、F分别在AD和AD的延长线上”改为“AB=kAC,点D在BC的延长线上,点E、F分别在DA和DA的延长线上”,其他条件不变(如图2).若CE=1,BF=3,∠BAC=α,求AF的长(用含k和α的式子表示).

(1)求证:∠AFB与∠BAC互补;
(2)图1中是否存在与AF相等的线段?若存在,请找出,并加以证明,若不存在,说明理由.
(3)若将“AB=AC,点D在BC上,点E、F分别在AD和AD的延长线上”改为“AB=kAC,点D在BC的延长线上,点E、F分别在DA和DA的延长线上”,其他条件不变(如图2).若CE=1,BF=3,∠BAC=α,求AF的长(用含k和α的式子表示).

考点:相似形综合题,平行线的性质,全等三角形的判定与性质,等腰三角形的判定与性质,相似三角形的判定与性质,锐角三角函数的定义
专题:压轴题
分析:(1)由BF∥CE得∠AFB=∠CEF,由∠AEC=∠BAC,∠CEF与∠AEC互补即可证到∠AFB与∠BAC互补.
(2)由图可猜想CE=AF.在AF上取一点G,使AG=BF,易证△ABF≌△CAG,从而有AF=CG,∠AFB=∠CGA;由∠AFB=∠CEF可得∠CGA=∠CEF,从而有CE=CG,则CE=AF.
(3)作∠GBA=∠EAC,点G在DA的延长线上,如图2,易证△GBA∽△EAC,从而有
=
=k,∠BGA=∠AEC=∠BAC=α.由BF∥CE可得∠BFG=180°-∠FEC=180°-α=∠BGF,从而有BG=BF.作BH⊥FG,垂足为H,如图2,可证到GF=2FH.从而可得AF=AG+GF=AG+2FH=kCE+2BFcos∠BFG=k+6cos(180°-α).
(2)由图可猜想CE=AF.在AF上取一点G,使AG=BF,易证△ABF≌△CAG,从而有AF=CG,∠AFB=∠CGA;由∠AFB=∠CEF可得∠CGA=∠CEF,从而有CE=CG,则CE=AF.
(3)作∠GBA=∠EAC,点G在DA的延长线上,如图2,易证△GBA∽△EAC,从而有
| AG |
| CE |
| AB |
| AC |
解答:(1)证明:如图1,∵BF∥CE,
∴∠AFB=∠CEF.
∵∠CEF与∠AEC互补,∠AEC=∠BAC,
∴∠CEF与∠BAC互补.
∴∠AFB与∠BAC互补.
(2)存在,CE=AF.
证明:在AF上取一点G,使AG=BF,如图1.
∵∠AFB+∠BAF+∠CAF=∠AFB+∠BAC=180°,
∠AFB+∠BAF+∠ABF=180°,
∴∠ABF=∠CAF.
在△ABF和△CAG中,
,
∴△ABF≌△CAG(SAS).
∴AF=CG,∠AFB=∠CGA.
又∵∠AFB=∠CEF,
∴∠CGA=∠CEF.
∴CE=CG.
∴CE=AF.
(3)解:作∠GBA=∠EAC,点G在DA的延长线上,如图2.
∵∠AEC=∠BAC,
∠GAB+∠BAC+∠EAC=180°,
∠ECA+∠AEC+∠EAC=180°,
∴∠GAB=∠ECA.
∵∠GBA=∠EAC,∠GAB=∠ECA,
∴△GBA∽△EAC.
∴
=
=k,∠BGA=∠AEC=∠BAC=α.
∴AG=kCE.
∵BF∥CE,
∴∠BFG=180°-∠FEC=180°-∠BGA=∠BGF,
∴BG=BF.
作BH⊥FG,垂足为H,如图2,
∵BG=BF,BH⊥FG,
∴GH=FH.
∴GF=2FH.
在Rt△BHF中,cos∠BFG=
,
∴FH=BF•cos∠BFG.
∵CE=1,BF=3,∠BAC=α,
∴AF=AG+GF
=AG+2FH
=kCE+2BFcos∠BFG
=k+6cos(180°-α).
∴AF的长为k+6cos(180°-α).
∴∠AFB=∠CEF.
∵∠CEF与∠AEC互补,∠AEC=∠BAC,
∴∠CEF与∠BAC互补.
∴∠AFB与∠BAC互补.
(2)存在,CE=AF.
证明:在AF上取一点G,使AG=BF,如图1.

∵∠AFB+∠BAF+∠CAF=∠AFB+∠BAC=180°,
∠AFB+∠BAF+∠ABF=180°,
∴∠ABF=∠CAF.
在△ABF和△CAG中,
|
∴△ABF≌△CAG(SAS).
∴AF=CG,∠AFB=∠CGA.
又∵∠AFB=∠CEF,
∴∠CGA=∠CEF.
∴CE=CG.
∴CE=AF.
(3)解:作∠GBA=∠EAC,点G在DA的延长线上,如图2.
∵∠AEC=∠BAC,
∠GAB+∠BAC+∠EAC=180°,
∠ECA+∠AEC+∠EAC=180°,
∴∠GAB=∠ECA.
∵∠GBA=∠EAC,∠GAB=∠ECA,
∴△GBA∽△EAC.
∴
| AG |
| CE |
| AB |
| AC |

∴AG=kCE.
∵BF∥CE,
∴∠BFG=180°-∠FEC=180°-∠BGA=∠BGF,
∴BG=BF.
作BH⊥FG,垂足为H,如图2,
∵BG=BF,BH⊥FG,
∴GH=FH.
∴GF=2FH.
在Rt△BHF中,cos∠BFG=
| FH |
| BF |
∴FH=BF•cos∠BFG.
∵CE=1,BF=3,∠BAC=α,
∴AF=AG+GF
=AG+2FH
=kCE+2BFcos∠BFG
=k+6cos(180°-α).
∴AF的长为k+6cos(180°-α).
点评:本题考查了平行线的性质、全等三角形的判定与性质、等腰三角形的判定与性质、相似三角形的判定与性质、锐角三角函数的定义等知识,综合性强,有一定的难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知:关于x的一元二次方程mx2-(m+3)x+3=0有两个不相等的实数根.
已知:关于x的一元二次方程mx2-(m+3)x+3=0有两个不相等的实数根.