题目内容
15.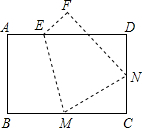 如图,将矩形ABCD沿EM折叠,使顶点B恰好落在CD边的中点N上.若AB=6,AD=9,则五边形ABMND的周长为( )
如图,将矩形ABCD沿EM折叠,使顶点B恰好落在CD边的中点N上.若AB=6,AD=9,则五边形ABMND的周长为( )| A. | 28 | B. | 26 | C. | 25 | D. | 22 |
分析 如图,运用矩形的性质首先证明CN=3,∠C=90°;运用翻折变换的性质证明BM=MN(设为λ),运用勾股定理列出关于λ的方程,求出λ,即可解决问题.
解答  解:如图,由题意得:BM=MN(设为λ),CN=DN=3;
解:如图,由题意得:BM=MN(设为λ),CN=DN=3;
∵四边形ABCD为矩形,
∴BC=AD=9,∠C=90°,MC=9-λ;
由勾股定理得:λ2=(9-λ)2+32,
解得:λ=5,
∴五边形ABMND的周长=6+5+5+3+9=28,
故选A.
点评 该题主要考查了翻折变换的性质、矩形的性质、勾股定理等几何知识点及其应用问题;解题的关键是灵活运用翻折变换的性质、矩形的性质、勾股定理等几何知识点来分析、判断、推理或解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.若点P在第四象限,且P到x轴的距离为1,到y轴的距离为2,则点P的坐标是( )
| A. | (-1,2) | B. | (1,-2) | C. | (-2,1) | D. | (2,-1) |
3.下列计算正确的是( )
| A. | a3+a2=a5 | B. | a3-a2=a | C. | a2•a4=a8 | D. | a3÷a2=a |
4.下列4个命题:①三点确定一个圆;②平分弦的直径平分弦所对的弧;③弦相等,所对的圆心角相等;④在半径为4的圆中,30°的圆心角所对的弧长为$\frac{2π}{3}$.其中真命题的个数有( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.已知三角形的两边长分别是4和7,则这个三角形的第三条边的长可能是( )
| A. | 12 | B. | 11 | C. | 8 | D. | 3 |
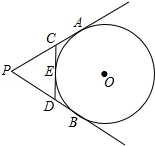 如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为r,△PCD的周长等于3r,则sin∠APB的值是$\frac{12}{13}$.
如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为r,△PCD的周长等于3r,则sin∠APB的值是$\frac{12}{13}$. 如图,D是线段AC的中点,E是线段AB的中点.已知AB=10,BC=3,求线段AD和DE的长度.
如图,D是线段AC的中点,E是线段AB的中点.已知AB=10,BC=3,求线段AD和DE的长度.