题目内容
7. 如图,D是线段AC的中点,E是线段AB的中点.已知AB=10,BC=3,求线段AD和DE的长度.
如图,D是线段AC的中点,E是线段AB的中点.已知AB=10,BC=3,求线段AD和DE的长度.
分析 根据线段的和差,可得AC的长,根据线段中点的性质,可得AD,AE的长,再根据线段的和差,可得答案.
解答 解:∵AB=10,BC=3
∴AC=AB-BC=7.
∵点D为AC的中点
∴AD=$\frac{1}{2}$AC=3.5.
∵点E是AB的中点,
∴AE=$\frac{1}{2}$AB=5,
∴DE=AE-AD=15.
点评 本题考查了两点间的距离,利用线段中点的性质得出AD,AE的长是解题关键.

练习册系列答案
相关题目
17.函数y=$\frac{x}{\sqrt{x+2}}$中x的取值范围为( )
| A. | x≥-2且x≠0 | B. | x>-2且x≠0 | C. | x>-2 | D. | x≠0 |
18. 如图,AB是⊙O的直径,CD是弦,AB⊥CD,垂足为点E,连接OD、CB、AC,∠ODE=30°,EB=2,那么CD的长为( )
如图,AB是⊙O的直径,CD是弦,AB⊥CD,垂足为点E,连接OD、CB、AC,∠ODE=30°,EB=2,那么CD的长为( )
 如图,AB是⊙O的直径,CD是弦,AB⊥CD,垂足为点E,连接OD、CB、AC,∠ODE=30°,EB=2,那么CD的长为( )
如图,AB是⊙O的直径,CD是弦,AB⊥CD,垂足为点E,连接OD、CB、AC,∠ODE=30°,EB=2,那么CD的长为( )| A. | 4$\sqrt{3}$ | B. | 5$\sqrt{3}$ | C. | 5$\sqrt{5}$ | D. | 6$\sqrt{2}$ |
15.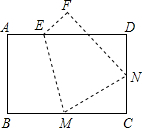 如图,将矩形ABCD沿EM折叠,使顶点B恰好落在CD边的中点N上.若AB=6,AD=9,则五边形ABMND的周长为( )
如图,将矩形ABCD沿EM折叠,使顶点B恰好落在CD边的中点N上.若AB=6,AD=9,则五边形ABMND的周长为( )
 如图,将矩形ABCD沿EM折叠,使顶点B恰好落在CD边的中点N上.若AB=6,AD=9,则五边形ABMND的周长为( )
如图,将矩形ABCD沿EM折叠,使顶点B恰好落在CD边的中点N上.若AB=6,AD=9,则五边形ABMND的周长为( )| A. | 28 | B. | 26 | C. | 25 | D. | 22 |
17.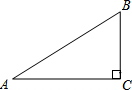 如图,已知在Rt△ABC中,∠C=90°,AC=4,tanA=$\frac{1}{2}$,则AB的长是( )
如图,已知在Rt△ABC中,∠C=90°,AC=4,tanA=$\frac{1}{2}$,则AB的长是( )
 如图,已知在Rt△ABC中,∠C=90°,AC=4,tanA=$\frac{1}{2}$,则AB的长是( )
如图,已知在Rt△ABC中,∠C=90°,AC=4,tanA=$\frac{1}{2}$,则AB的长是( )| A. | 2 | B. | 8 | C. | 2$\sqrt{5}$ | D. | 4$\sqrt{5}$ |
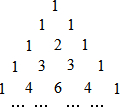 如图所示的“贾宪三角”告诉了我们二项式乘方展开式的系数规律,如:第四行的四个数恰好对应着(a+b)3的展开式a3+3a2b+3ab2+b3的系数; 第五行的五个数恰好对应着(a+b)4的展开式a4+4a3b+6a2b2+4ab3+b4的系数;
如图所示的“贾宪三角”告诉了我们二项式乘方展开式的系数规律,如:第四行的四个数恰好对应着(a+b)3的展开式a3+3a2b+3ab2+b3的系数; 第五行的五个数恰好对应着(a+b)4的展开式a4+4a3b+6a2b2+4ab3+b4的系数;