题目内容
6.若点(3,4)是反比例函数y=$\frac{2m-2}{x}$图象上一点,则此函数图象必须经过点( )| A. | (2,6) | B. | (2,-6) | C. | (4,-3) | D. | (3,-4) |
分析 据反比例函数图象上点的坐标特征,将点(3,4)代入反比例函数y=$\frac{2m-2}{x}$,求得2m-2值,然后再求函数图象所必须经过的点.
解答 解:∵点(3,4)是反比例函数y=$\frac{2m-2}{x}$图象上一点,
∴点(3,4)满足反比例函数y=$\frac{2m-2}{x}$,
∴4=$\frac{2m-2}{3}$,即2m-2=12,
∴点(3,4)是反比例函数为y=$\frac{12}{x}$上的一点,
∴xy=12;
A、∵x=2,y=6,∴2×6=12,故本选项正确;
B、∵x=2,y=-6,∴2×(-6)=-12,故本选项错误;
C、∵x=4,y=-3,∴4×(-3)=-12,故本选项错误;
D、∵x=3,y=-4,∴3×(-4)=-12,故本选项错误.
故选:A.
点评 本题主要考查反比例函数图象上点的坐标特征,所有在反比例函数上的点的横纵坐标的积应等于比例系数.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
14.一组数据:-3,1,4,1,-3,则这组数据的中位数是( )
| A. | -3 | B. | 1 | C. | 3 | D. | 4 |
1.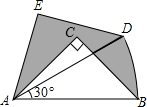 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE,点B经过的路径为BD,则图中阴影部分的面积是( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE,点B经过的路径为BD,则图中阴影部分的面积是( )
 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE,点B经过的路径为BD,则图中阴影部分的面积是( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE,点B经过的路径为BD,则图中阴影部分的面积是( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{3}$ |
15.如果(4a2-3ab2)÷M=-4a+3b2,那么单项式M等于( )
| A. | ab | B. | -ab | C. | -a | D. | -b |
 如图,平行四边形ABCD对角线交于点O,若AC=6cm,BC=10cm,BD=24cm,则△OBC的周长为25cm.
如图,平行四边形ABCD对角线交于点O,若AC=6cm,BC=10cm,BD=24cm,则△OBC的周长为25cm. 如图,正方形ABCD中,以对角线AC为一边作菱形AEFC,则∠FAB=22.5°.
如图,正方形ABCD中,以对角线AC为一边作菱形AEFC,则∠FAB=22.5°.