题目内容
14.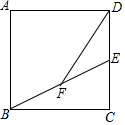 如图,在正方形ABCD中,点E是CD中点,点F是BE的中点,若AB=4,则DF=$\sqrt{13}$.
如图,在正方形ABCD中,点E是CD中点,点F是BE的中点,若AB=4,则DF=$\sqrt{13}$.
分析 如图,作FM⊥CD于M.只要证明FN是△EBC的中位线,在Rt△DFM中,利用勾股定理即可解决问题.
解答 解:如图,作FM⊥CD于M.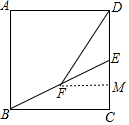
∵四边形ABCD是正方形,
∴AB=BC=CD=4,∠C=∠FME=90°,
∴FM∥BC,
∵BF=EF,
∴EM=MC,
∴FM=$\frac{1}{2}$BC=2,
在Rt△DFM中,∵∠FMD=90°,FM=2,DM=DE+EM=2+1=3,
∴DF=$\sqrt{F{M}^{2}+D{M}^{2}}$=$\sqrt{13}$,
故答案为$\sqrt{13}$.
点评 本题考查正方形的性质、三角形的中位线定理、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
19.使分式$\frac{x+2}{x-1}$有意义的x的取值范围是( )
| A. | x≠-1 | B. | x≠1 | C. | x>-1 | D. | x<1 |
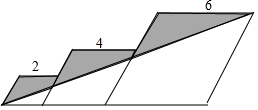 如图,三个均含有一个60°内角且边长分别为2,4,6的菱形在同一水平线上依次排列,则图中阴影部分的面积为10$\sqrt{3}$.
如图,三个均含有一个60°内角且边长分别为2,4,6的菱形在同一水平线上依次排列,则图中阴影部分的面积为10$\sqrt{3}$. 如图,在Rt△ABC中,∠BAC=90°,∠B=60°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F.
如图,在Rt△ABC中,∠BAC=90°,∠B=60°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F. 如图,点A、B是函数y=$\frac{k}{x}$的图象上关于原点对称的任意两点,BC∥x轴,AC∥y轴,△ABC的面积为4,则k=2.
如图,点A、B是函数y=$\frac{k}{x}$的图象上关于原点对称的任意两点,BC∥x轴,AC∥y轴,△ABC的面积为4,则k=2. 如图,△ABC中,∠ABC=90°,AB=BC,点E、F在AC上,∠EBF=45°,若AE=1,CF=2,则AB的长为$\frac{3\sqrt{2}+\sqrt{10}}{2}$.
如图,△ABC中,∠ABC=90°,AB=BC,点E、F在AC上,∠EBF=45°,若AE=1,CF=2,则AB的长为$\frac{3\sqrt{2}+\sqrt{10}}{2}$.