题目内容
4.先化简,再求值:($\frac{1}{x+1}$-$\frac{1}{1-x}$)÷$\frac{{x}^{2}}{1-{x}^{2}}$,其中x=$\sqrt{2}$+1.分析 先化简题目中的式子,然后将x的值代入化简后的式子即可解答本题.
解答 解:($\frac{1}{x+1}$-$\frac{1}{1-x}$)÷$\frac{{x}^{2}}{1-{x}^{2}}$
=$\frac{1-x-(1+x)}{(1+x)(1-x)}•\frac{(1+x)(1-x)}{{x}^{2}}$
=$\frac{-2x}{{x}^{2}}$
=$-\frac{2}{x}$,
当x=$\sqrt{2}+1$时,原式=-$\frac{2}{\sqrt{2}+1}$=-2$\sqrt{2}$+2.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.利用计算机设计了一个计算程序,输入和输出的数据如下表:
当输入的数据是8时,输出的数据是-$\frac{8}{65}$,当输入数据是n时,输出的数据是(-1)n+1$\frac{n}{{n}^{2}+1}$.
| 输入 | … | 1 | 2 | 3 | 4 | 5 | … |
| 输出 | … | $\frac{1}{2}$ | $-\frac{2}{5}$ | $\frac{3}{10}$ | -$\frac{4}{17}$ | $\frac{5}{26}$ | … |
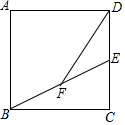 如图,在正方形ABCD中,点E是CD中点,点F是BE的中点,若AB=4,则DF=$\sqrt{13}$.
如图,在正方形ABCD中,点E是CD中点,点F是BE的中点,若AB=4,则DF=$\sqrt{13}$.
 为了解某小区家庭用水情况,小丽随机调查了该小区部分家庭4月份的用水量,并将收集的数据整理并绘制成如下条形统计图.
为了解某小区家庭用水情况,小丽随机调查了该小区部分家庭4月份的用水量,并将收集的数据整理并绘制成如下条形统计图.

