题目内容
3. 如图,△ABC中,∠ABC=90°,AB=BC,点E、F在AC上,∠EBF=45°,若AE=1,CF=2,则AB的长为$\frac{3\sqrt{2}+\sqrt{10}}{2}$.
如图,△ABC中,∠ABC=90°,AB=BC,点E、F在AC上,∠EBF=45°,若AE=1,CF=2,则AB的长为$\frac{3\sqrt{2}+\sqrt{10}}{2}$.
分析 将△ABE绕点B顺时针旋转90°得到△CBH.连接FH.只要证明△FBH≌△FBE,再证明∠FCH=90°,求出FH即可解决问题.
解答 解:将△ABE绕点B顺时针旋转90°得到△CBH.连接FH.
∵∠EBF=45°,∠ABC=90°,
∴∠ABE+∠CBF=45°,
∵∠ABE=∠CBH,
∴∠CBH+∠CBF=45°,
∴∠FBH=∠FBE=45°,
在△FBH和△FBE中,
$\left\{\begin{array}{l}{FB=FB}\\{∠FBH=∠FBE}\\{BH=BE}\end{array}\right.$,
∴△FBH≌△FBE,
∴FH=EF,
∵∠BCF=∠BCH=45°,
∴∠FCH=90°,
∴EF=FH=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∴AC=3+$\sqrt{5}$,
∴AB=AC•cos45°=$\frac{3\sqrt{2}+\sqrt{10}}{2}$,
故答案为$\frac{3\sqrt{2}+\sqrt{10}}{2}$
点评 本题考查了图形的旋转,全等三角形的性质和判定,三角形内角和定理,等腰直角三角形的性质的应用,能正确作出辅助线是解此题的关键.

练习册系列答案
相关题目
13. 如图,直线y=-x+3与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=3BO,则反比例函数的解析式为( )
如图,直线y=-x+3与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=3BO,则反比例函数的解析式为( )
 如图,直线y=-x+3与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=3BO,则反比例函数的解析式为( )
如图,直线y=-x+3与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=3BO,则反比例函数的解析式为( )| A. | y=$\frac{2}{x}$ | B. | y=-$\frac{2}{x}$ | C. | y=$\frac{4}{x}$ | D. | y=-$\frac{4}{x}$ |
11.下列各式中,是3x2y的同类项的是( )
| A. | 3a2b | B. | -2xy2 | C. | x2y | D. | 3xy |
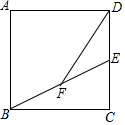 如图,在正方形ABCD中,点E是CD中点,点F是BE的中点,若AB=4,则DF=$\sqrt{13}$.
如图,在正方形ABCD中,点E是CD中点,点F是BE的中点,若AB=4,则DF=$\sqrt{13}$. 如图,用四条线段首尾相接连成一个框架,其中AB=12,BC=14,CD=18,DA=24,则A、B、C、D任意两点之间的最长距离为( )
如图,用四条线段首尾相接连成一个框架,其中AB=12,BC=14,CD=18,DA=24,则A、B、C、D任意两点之间的最长距离为( )

 为了解某小区家庭用水情况,小丽随机调查了该小区部分家庭4月份的用水量,并将收集的数据整理并绘制成如下条形统计图.
为了解某小区家庭用水情况,小丽随机调查了该小区部分家庭4月份的用水量,并将收集的数据整理并绘制成如下条形统计图.