题目内容
5.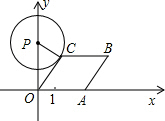 如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,以O、A为顶点作菱形OABC,使B、C点都在第一象限内,且∠AOC=60°.设经过t秒后,以P(0,3)为圆心,PC为半径的圆恰好与菱形OABC的边所在的直线相切,则t=$\frac{3\sqrt{3}}{2}$-1或$3\sqrt{3}-1$.
如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,以O、A为顶点作菱形OABC,使B、C点都在第一象限内,且∠AOC=60°.设经过t秒后,以P(0,3)为圆心,PC为半径的圆恰好与菱形OABC的边所在的直线相切,则t=$\frac{3\sqrt{3}}{2}$-1或$3\sqrt{3}-1$.
分析 分情况讨论①先由切线的性质得出∠OCP=90°,再由已知条件得出∠POC=30°,根据三角函数求出OC,由菱形性质得出OA=OC,即可得出t;②当∠OCP=30°时,圆与OA所在直线相切,同理求得t.
解答 解:∵当以P(0,3)为圆心,PC为半径的圆恰好与菱形OABC的边OC所在的直线相切,
∴∠OCP=90°,
∵∠AOC=60°,
∴∠POC=30°,
∴OC=OP•cos30°=3×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$,
∵四边形OABC是菱形,
∴OA=OC=$\frac{3\sqrt{3}}{2}$,
∴t=$\frac{3\sqrt{3}}{2}$-1;
同理当以P(0,3)为圆心,PC为半径的圆恰好与菱形OABC的边OA所在的直线相切时,求得t=$3\sqrt{3}-1$
故答案为:$\frac{3\sqrt{3}}{2}$-1或$3\sqrt{3}-1$.
点评 本题考查了切线的性质、菱形的性质、坐标与图形性质以及锐角三角函数;运用三角函数求出菱形的边长是解决问题的关键.

练习册系列答案
相关题目
20.意大利著名数学家芬波那在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数值起,每一个数都等于它前面两个数的和,现以这组数中的各个数作为正方形的边长值构造如下正方形:
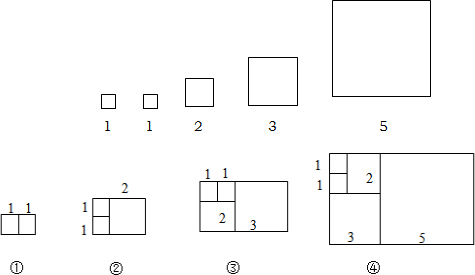
两分别依次从左到右取2个、3个、4个、5个…正方形拼成如下长方形并记为①、②、③、④、…相应长方形的周长如表所示:
(1)仔细观察图形,表中的x=16,y=26;
(2)若按此规律继续拼成长方形,则序号为④的长方形周长是26(并写出简要的过程)
(3)以下①、②小题只需选做一小题,若两小题都写,则只按第①小题的解答给分.
①若按此规律拼长方形,已知序号为n的长方形的周长为a,序号为(n+1)的长方形的周长为b,则序号为(n+3)的长方形的周长为a+2b(用含a、b的代数式表示)
②若按此规律继续拼长方形,已知序号为n的长方形的长和宽分别为a、b(其中a<b),则序号为(n+1)的长方形的周长是2a+4b(用含a、b的代数式表示).

两分别依次从左到右取2个、3个、4个、5个…正方形拼成如下长方形并记为①、②、③、④、…相应长方形的周长如表所示:
| 序号 | ① | ② | ③ | ④ | … |
| 周长 | 6 | 10 | x | y | … |
(2)若按此规律继续拼成长方形,则序号为④的长方形周长是26(并写出简要的过程)
(3)以下①、②小题只需选做一小题,若两小题都写,则只按第①小题的解答给分.
①若按此规律拼长方形,已知序号为n的长方形的周长为a,序号为(n+1)的长方形的周长为b,则序号为(n+3)的长方形的周长为a+2b(用含a、b的代数式表示)
②若按此规律继续拼长方形,已知序号为n的长方形的长和宽分别为a、b(其中a<b),则序号为(n+1)的长方形的周长是2a+4b(用含a、b的代数式表示).
14.下列命题中假命题是( )
| A. | 平分弦的半径垂直于弦 | |
| B. | 垂直平分弦的直线必经过圆心 | |
| C. | 垂直于弦的直径平分这条弦所对的弧 | |
| D. | 平分弧的直径垂直平分这条弧所对的弦 |
15.某工地因道路建设需要开挖土石方,计划每小时挖掘土石方540m3,现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如表:
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案.
| 租金(单位:元/台•时) | 挖掘土石方量(单位:m3/台•时) | |
| 甲型机 | 100 | 60 |
| 乙型机 | 120 | 80 |
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案.
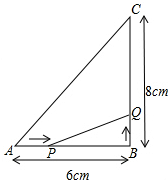 如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.