题目内容
16.阅读下面例题的解答过程,体会并其方法,并借鉴例题的解法解方程.例:解方程x2-|x-1|-1=0.
解:(1)当x-1≥0即x≥1时,|x-1|=x-1.
原化为方程x2-(x-1)-1=0,即x2-x=0
解得x1=0.x2=1
∵x≥1,故x=0舍去,
∴x=1是原方程的解.
(2)当x-1<0即x<1时,|x-1|=-(x-1).
原化为方程x2+(x-1)-1=0,即x2+x-2=0
解得x1=1.x2=-2
∵x<1,故x=1舍去,
∴x=-2是原方程的解.
综上所述,原方程的解为x1=1,x2=-2
解方程x2-|x-2|-4=0.
分析 先要去绝对值,把方程化为一元二次方程,则分类讨论:(1)当x-2≥0即x≥2时,原化为方程x2-(x-2)-4=0,即x2-x-2=0;(2)当x-2<0即x<2时,原化为方程x2+(x-2)-4=0,即x2+x-6=0,然后利用因式分解法解两个一元二次方程,再根据x的取值范围确定原方程的解.
解答 解:(1)当x-2≥0即x≥2时,|x-2|=x-2.
原化为方程x2-(x-2)-4=0,即x2-x-2=0
解得x1=2.x2=-1,
∵x≥2,故x=-1舍去,
∴x=2是原方程的解.
(2)当x-2<0即x<2时,|x-2|=-(x-2).
原化为方程x2+(x-2)-4=0,即x2+x-6=0
解得x1=2.x2=-3,
∵x<2,故x=2舍去,
∴x=-3是原方程的解.
综上所述,原方程的解为x1=2,x2=-3.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
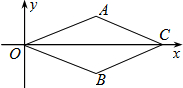 如图,在平面直角坐标系中,菱形OABC的顶点O、A的坐标分别是(0,0),(2,1),则顶点C的坐标是(4,0).
如图,在平面直角坐标系中,菱形OABC的顶点O、A的坐标分别是(0,0),(2,1),则顶点C的坐标是(4,0).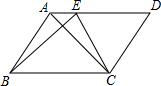 已知,如图,?ABCD中,E是边AD上任意一点,求证:S△ABC=S△EBC.
已知,如图,?ABCD中,E是边AD上任意一点,求证:S△ABC=S△EBC.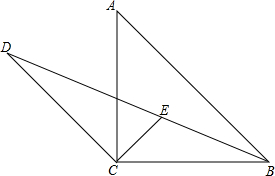 在△ABC中,∠ACB=90°,AC=BC,过C作CD∥AB交∠ABC的平分线于点D,∠ACB的平分线交BD于点E.
在△ABC中,∠ACB=90°,AC=BC,过C作CD∥AB交∠ABC的平分线于点D,∠ACB的平分线交BD于点E.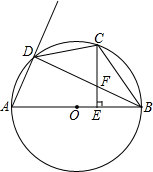 如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.
如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.
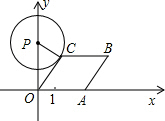 如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,以O、A为顶点作菱形OABC,使B、C点都在第一象限内,且∠AOC=60°.设经过t秒后,以P(0,3)为圆心,PC为半径的圆恰好与菱形OABC的边所在的直线相切,则t=$\frac{3\sqrt{3}}{2}$-1或$3\sqrt{3}-1$.
如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,以O、A为顶点作菱形OABC,使B、C点都在第一象限内,且∠AOC=60°.设经过t秒后,以P(0,3)为圆心,PC为半径的圆恰好与菱形OABC的边所在的直线相切,则t=$\frac{3\sqrt{3}}{2}$-1或$3\sqrt{3}-1$.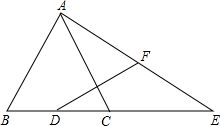 如图,已知在△ABC中,AB=AC=2$\sqrt{5}$,sin∠B=$\frac{2\sqrt{5}}{5}$,D为边BC的中点,E为边BC的延长线上一点,且CE=BC.联结AE,F为线段AE的中点.
如图,已知在△ABC中,AB=AC=2$\sqrt{5}$,sin∠B=$\frac{2\sqrt{5}}{5}$,D为边BC的中点,E为边BC的延长线上一点,且CE=BC.联结AE,F为线段AE的中点.