题目内容
7.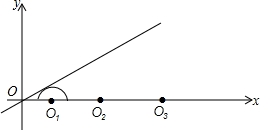 如图,圆心都在x轴正半轴上的半圆O1,半圆O2,…,半圆
如图,圆心都在x轴正半轴上的半圆O1,半圆O2,…,半圆On与直线L相切.设半圆O1,半圆O2,…,半圆On的半径分别是r1,r2,…,rn,则当直线L与x轴所成锐角为30°,且r1=1时,r2015=32014.
分析 分别作O1A⊥l,O2B⊥l,O3C⊥l,如图,根据切线的性质得O1A=r1,O2B=r2,O3C=r3,再利用含30度的直角三角形三边的关系得到OO1=2O1A=2r1=2,在Rt△OO2B中,OO2=2O2B,即2+1+r2=2r2,解得r2=3,同理得到r3=9=32,按此规律同理可得rn=3n-1,然后n取2015即可得到答案.
解答 解:分别作O1A⊥l,O2B⊥l,O3C⊥l,如图,
∵半圆O1,半圆O2,…,半圆On与直线L相切,
∴O1A=r1,O2B=r2,O3C=r3,
∵∠AOO1=30°,
∴OO1=2O1A=2r1=2,
在Rt△OO2B中,OO2=2O2B,即2+1+r2=2r2,
∴r2=3,
在Rt△OO2C中,OO3=2O2C,即2+1+2×3++r3=2r3,
∴r3=9=32,
同理可得r4=27=33,
所以r2015=32014.
故答案为32014.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了从特殊到一般的方法解决规律型问题.

练习册系列答案
相关题目
12.甲.乙两车分别从A、B两地同时出发,相向而行,若快车甲的速度为60km/h,慢车乙的速度比快车甲慢4km/h,A、B两地相距80km,求两车出发到相遇所行时间.如果设xh后两车相遇,则根据题意列出方程( )
| A. | $\frac{x}{80}$+$\frac{x-4}{80}$=60 | B. | x(x-4)=80 | C. | 60x+(60-4)x=80 | D. | 60x+60(x-4)=80 |
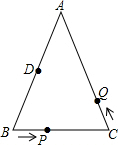 如图,△ABC中,AB=AC=12cm,BC=8cm,点D为AB的中点.如果点P在BC上以2cm/s的速度由B→C运动,同时,点Q在AC上以相同的速度由C→A运动,当点P到达点C或点Q到达点A时运动停止.
如图,△ABC中,AB=AC=12cm,BC=8cm,点D为AB的中点.如果点P在BC上以2cm/s的速度由B→C运动,同时,点Q在AC上以相同的速度由C→A运动,当点P到达点C或点Q到达点A时运动停止.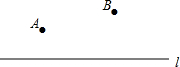 如图,已知直线l及其同侧两点A、B.
如图,已知直线l及其同侧两点A、B.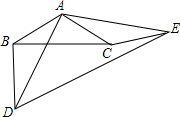 如图所示,△ABC,△ADE均是顶角为120°的等腰三角形,BC,DE分别是它们的底边,图中的哪两个三角形可以通过怎样的旋转而相互得到?
如图所示,△ABC,△ADE均是顶角为120°的等腰三角形,BC,DE分别是它们的底边,图中的哪两个三角形可以通过怎样的旋转而相互得到?