题目内容
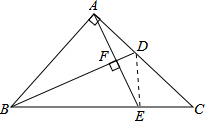
 已知:如图,在△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC,交AC于D,AE⊥BD于F,交BC于E.求证:
已知:如图,在△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC,交AC于D,AE⊥BD于F,交BC于E.求证:(1﹚AB=BE;
(2﹚∠CAE=
| 1 |
| 2 |
(3﹚AD=CE;
(4﹚CD+CE=AB.
考点:全等三角形的判定与性质,角平分线的性质,等腰直角三角形
专题:证明题
分析:(1)BD平分∠ABC,AE⊥BD,BF为公共边,可证得△ABF≌△EBF,可证得结论;
(2)∠BAC=90°可得∠CAE+∠BAF=90°,而∠BAF+∠ABF=90°,所以∠CAE=
∠ABC;
(3)连接DE,则可证得△ABD≌△EBD,所以AD=DE,且∠DEC=90°,AB=AC,所以∠C=45°,所以CE=DE,所以可得AD=CE;
(4)由(3)可得AD=CE,所以CD+AD=CD+CE=AC=AB.
(2)∠BAC=90°可得∠CAE+∠BAF=90°,而∠BAF+∠ABF=90°,所以∠CAE=
| 1 |
| 2 |
(3)连接DE,则可证得△ABD≌△EBD,所以AD=DE,且∠DEC=90°,AB=AC,所以∠C=45°,所以CE=DE,所以可得AD=CE;
(4)由(3)可得AD=CE,所以CD+AD=CD+CE=AC=AB.
解答:证明:(1)∵BD平分∠ABC,AE⊥BD,
∴∠ABF=∠EBF,∠AFB=∠EFB=90°,
在△ABF和△EBF中,
,
∴△ABF≌△EBF(AAS),
∴AB=BE;
(2)∵∠BAC=90°,
∴∠CAE+∠BAF=90°,而∠BAF+∠ABF=90°,
∴∠CAE=∠ABF=
∠ABC;
(3)连接DE,
在△ABD和△EBD中
,
∴△ABD≌△EBD(SAS),
∴AD=DE,∠DEC=∠BAC=90°,
∵∠BAC=90°,AB=AC,
∴∠C=45°,
∴CE=DE,
∴AD=CE;
(4)由(3)可得AD=CE,
所以CD+AD=CD+CE=AC=AB.
∴∠ABF=∠EBF,∠AFB=∠EFB=90°,
在△ABF和△EBF中,
|
∴△ABF≌△EBF(AAS),
∴AB=BE;
(2)∵∠BAC=90°,
∴∠CAE+∠BAF=90°,而∠BAF+∠ABF=90°,
∴∠CAE=∠ABF=
| 1 |
| 2 |
(3)连接DE,

在△ABD和△EBD中
|
∴△ABD≌△EBD(SAS),
∴AD=DE,∠DEC=∠BAC=90°,
∵∠BAC=90°,AB=AC,
∴∠C=45°,
∴CE=DE,
∴AD=CE;
(4)由(3)可得AD=CE,
所以CD+AD=CD+CE=AC=AB.
点评:本题主要考查三角形全等的判定和性质,注意观察所求线段或角之间的关系,找到所在的两个三角形,证明全等即可解决.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
在数轴上与原点的距离等于4的点表示的数是( )
| A、4. | B、-4 |
| C、4或-4 | D、无数个 |
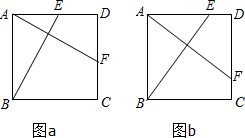 如图ABCD是一个正方形花园.E、F是它的两个门且分别是AD、CD的中点,要修两条路BE和AF
如图ABCD是一个正方形花园.E、F是它的两个门且分别是AD、CD的中点,要修两条路BE和AF 如图,用3个边长为1的正方形组成一个对称图形,则能将其完全覆盖的圆的最小半径为
如图,用3个边长为1的正方形组成一个对称图形,则能将其完全覆盖的圆的最小半径为