题目内容
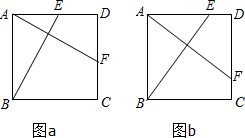 如图ABCD是一个正方形花园.E、F是它的两个门且分别是AD、CD的中点,要修两条路BE和AF
如图ABCD是一个正方形花园.E、F是它的两个门且分别是AD、CD的中点,要修两条路BE和AF1)如图a,这两条路等长吗?它们有什么位置关系?为什么?
2)如图b,若点E、F不是正方形ABCD的边的中点但满足DE=CF,那么这两条路等长吗?它们有什么位置关系?为什么?
考点:全等三角形的应用,正方形的性质
专题:
分析:(1)这条路等长,位置关系是垂直,根据正方形的性质证明△ADF≌△BAE,所以可得BE=AF,进而证明BE⊥AF;
(2)这条路等长,位置关系是垂直,根据(1)的思路证明△ADF≌△BAE即可.
(2)这条路等长,位置关系是垂直,根据(1)的思路证明△ADF≌△BAE即可.
解答:1)解:这条路等长,位置关系是垂直,
理由如下:
∵四边形ABCD是一个正方形,
∴AB=AD=CD,∠D=∠BAE=90°,
∵E、F分别是AD、CD的中点,
∴AE=DF,
在△ADF和△BAE中,
,
∴△ADF≌△BAE,
∴BE=AF,∠ABE=∠FAD,
∵∠ABE+∠AEB=90°,
∴∠FAD+∠AEB=90°,
∴BE⊥AF.
故BE=AF,BE⊥AF;
2)这条路等长,位置关系是垂直,
理由如下:
∵四边形ABCD是一个正方形,
∴AB=AD=CD,∠D=∠BAE=90°,
∵DE=CF,
∴AE=DF,
在△ADF和△BAE中,
,
∴△ADF≌△BAE,
∴BE=AF,∠ABE=∠FAD,
∵∠ABE+∠AEB=90°,
∴∠FAD+∠AEB=90°,
∴BE⊥AF.
故BE=AF,BE⊥AF.
理由如下:
∵四边形ABCD是一个正方形,

∴AB=AD=CD,∠D=∠BAE=90°,
∵E、F分别是AD、CD的中点,
∴AE=DF,
在△ADF和△BAE中,
|
∴△ADF≌△BAE,
∴BE=AF,∠ABE=∠FAD,
∵∠ABE+∠AEB=90°,
∴∠FAD+∠AEB=90°,
∴BE⊥AF.
故BE=AF,BE⊥AF;
2)这条路等长,位置关系是垂直,
理由如下:
∵四边形ABCD是一个正方形,

∴AB=AD=CD,∠D=∠BAE=90°,
∵DE=CF,
∴AE=DF,
在△ADF和△BAE中,
|
∴△ADF≌△BAE,
∴BE=AF,∠ABE=∠FAD,
∵∠ABE+∠AEB=90°,
∴∠FAD+∠AEB=90°,
∴BE⊥AF.
故BE=AF,BE⊥AF.
点评:本题考查了正方形的性质,全等三角形的判定和性质以及垂直的判定,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
式子2a-1可以化为( )
A、
| ||
B、
| ||
| C、-2a | ||
| D、2a-1 |
 如图所示,有一块地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,则这块地的面积.
如图所示,有一块地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,则这块地的面积. 已知:如图,在△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC,交AC于D,AE⊥BD于F,交BC于E.求证:
已知:如图,在△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC,交AC于D,AE⊥BD于F,交BC于E.求证: 如图,把△ABC的点A平移到点A1(-2,4),
如图,把△ABC的点A平移到点A1(-2,4), 如图,在五边形ABCDE中,M、N分别是AB、AE的中点,四边形AMPN,
如图,在五边形ABCDE中,M、N分别是AB、AE的中点,四边形AMPN,