题目内容
如图，用3个边长为1的正方形组成一个对称图形，则能将其完全覆盖的圆的最小半径为考点：垂径定理,勾股定理
专题：
分析：根据题意画出图形，连接OC，OD，延长BO交上面的正方形与点A，设定圆心与上面正方形的距离为x，再根据勾股定理求出x的值，进而可得出结论．
解答：
解：连接OC，OD，延长BO交上面的正方形与点A，设定圆心与上面正方形的距离为x，
则BO=1-x，BC=1，AD=0.5，AO=1+x，
故BC2+BO2=AD2+AO2，即1+（1-x）2=（1+x）2+0.52，（两边都是圆半径的平方）
解得，x=
，
所以能将其完全覆盖的圆的最小半径R2=1+（1-x）2，
解得R=
．
故答案为：
．
解：连接OC，OD，延长BO交上面的正方形与点A，设定圆心与上面正方形的距离为x，则BO=1-x，BC=1，AD=0.5，AO=1+x，
故BC2+BO2=AD2+AO2，即1+（1-x）2=（1+x）2+0.52，（两边都是圆半径的平方）
解得，x=
| 3 |
| 16 |
所以能将其完全覆盖的圆的最小半径R2=1+（1-x）2，
解得R=
5
| ||
| 16 |
故答案为：
5
| ||
| 16 |
点评：本题考查的是垂径定理，根据题意画出图形，利用数形结合进行解答是解答此题的关键．
练习册系列答案
孟建平错题本系列答案
超能学典应用题题卡系列答案
相关题目
已知：如图，在△ABC中，∠BAC=90°，AB=AC，BD平分∠ABC，交AC于D，AE⊥BD于F，交BC于E．求证：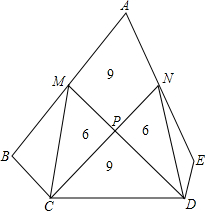
如图，在五边形ABCDE中，M、N分别是AB、AE的中点，四边形AMPN，
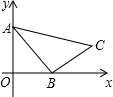如图，在Rt△ABC中，∠ABC=90°，AB=2，BC=
在△ABC中，已知AB=AC=5，BC=6，点D、E分别在边BC、AC上，且∠ADE=∠B，当BD的长为若关于x的二次三项式x2-mx+4是完全平方式，则（ ）
| A、m=4 | B、m=-4 |
| C、m=±4 | D、m=±2 |