题目内容
19.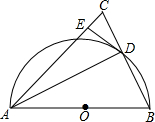 如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD.过点D作DE⊥AC,垂足为点E.
如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD.过点D作DE⊥AC,垂足为点E.(1)求证:DE是⊙O的切线;
(2)求证:BD2=AB•CE.
分析 (1)连接OD,AB为⊙0的直径得∠ADB=90°,由AB=AC,根据等腰三角形性质得AD平分BC,即DB=DC,则OD为△ABC的中位线,所以OD∥AC,而DE⊥AC,则OD⊥DE,然后根据切线的判定方法即可得到结论;
(2)由∠B=∠C,∠CED=∠BDA=90°,得出△DEC∽△ADB,得出$\frac{CE}{BD}$=$\frac{CD}{AB}$,从而求得BD•CD=AB•CE,由BD=AD,即可求得BD2=AB•CE.
解答 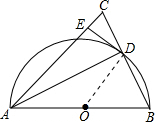 (1)证明:连接OD,如图,
(1)证明:连接OD,如图,
∵AB为⊙0的直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴AD平分BC,即DB=DC,
∵OA=OB,
∴OD为△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∴DE是⊙0的切线;
(2)证明:∵∠B=∠C,∠CED=∠BDA=90°,
∴△DEC∽△ADB,
∴$\frac{CE}{BD}$=$\frac{CD}{AB}$,
∴BD•CD=AB•CE,
∵BD=AD,
∴BD2=AB•CE.
点评 本题考查了切线的判定定理:过半径的外端点且与半径垂直的直线为圆的切线.也考查了等腰三角形的性质、三角形相似的判定和性质.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
4.下面是由数字组成的4个图形,其中能看到轴对称的图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.两数之和为18,其中一个数比另一个数的3倍还大2,若设大数为x,则列出的方程是( )
| A. | x-2=3(18-x) | B. | x+2=3(18-x) | C. | x+2=3(18+x) | D. | x-2=3(18+x) |
 几何证明:
几何证明: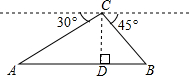 马航MH370失联以来,中国政府高度重视,每天军方派遣多架飞机、多艘军舰进行海上联合搜寻,某一天,从飞机C处测得A、B两艘军舰的俯角分别为30°、45°,此时飞机C处的高度CD为400米,点A,D,B在同一直线上,则A、B两艘军舰的距离是400($\sqrt{3}$+1)米.(结果保留根号)
马航MH370失联以来,中国政府高度重视,每天军方派遣多架飞机、多艘军舰进行海上联合搜寻,某一天,从飞机C处测得A、B两艘军舰的俯角分别为30°、45°,此时飞机C处的高度CD为400米,点A,D,B在同一直线上,则A、B两艘军舰的距离是400($\sqrt{3}$+1)米.(结果保留根号) 已知线段AB.请你以线段AB为斜边作Rt△ABP、Rt△ABQ,并判断点A、B、P、Q在同一个圆上,为什么?
已知线段AB.请你以线段AB为斜边作Rt△ABP、Rt△ABQ,并判断点A、B、P、Q在同一个圆上,为什么?