题目内容
如图，Rt△ABC中，∠C=90°，AC=6，BC=8，分别以AB，BC为边在AB的同侧作正方形ABRF，ACPQ，BDEC，四块阴影部分的面积分别为S1，S2，S3，S4，则S1+S2+S3+S4等于（ ）| A、42 | B、64 | C、72 | D、80 |
考点：勾股定理
专题：
分析：过F作AM的垂线交AM于D，通过证明S1+S2+S3+S4=Rt△ABC的面积×3，依此即可求解．
解答：
解：图中S4=SRt△ABC．S3=S△FPT，
∴S1+S3=SRt△ABC．
S2的左上方的顶点为F，过F作AM的垂线交AM于D，可证明Rt△ADF≌Rt△ABC，而图中Rt△DFK全等于①，
所以S2=SRt△ABC．
S1+S2+S3+S4
=（S1+S3）+S2+S4
=Rt△ABC的面积+Rt△ABC的面积+Rt△ABC的面积
=Rt△ABC的面积×3
=8×6÷2×3
=72．
故选：C．
解：图中S4=SRt△ABC．S3=S△FPT，∴S1+S3=SRt△ABC．
S2的左上方的顶点为F，过F作AM的垂线交AM于D，可证明Rt△ADF≌Rt△ABC，而图中Rt△DFK全等于①，
所以S2=SRt△ABC．
S1+S2+S3+S4
=（S1+S3）+S2+S4
=Rt△ABC的面积+Rt△ABC的面积+Rt△ABC的面积
=Rt△ABC的面积×3
=8×6÷2×3
=72．
故选：C．
点评：本题考查勾股定理的知识，有一定难度，解题关键是将勾股定理和正方形的面积公式进行灵活的结合和应用．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
如图所示，?ABCD中，E、F是对角线AC上的两点，且AF=CE．
如图，两个反比例函数y=直角三角形的两直角边为a，b，斜边为c，则下列关于a，b，c三边关系不正确的是（ ）
| A、a2+b2=c2 |
| B、b2=c2-a2 |
| C、a2=c2-b2 |
| D、b2=a2-c2 |
下列运算正确的是（ ）
| A、（ab）2=ab2 | ||||||
| B、（a3）2=a5 | ||||||
C、
| ||||||
D、
|
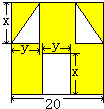“囧”（jiong）是最近时期网络流行语，像一个人脸郁闷的神情．如图所示，一张边长为20的正方形的纸片，剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案（阴影部分）．设剪去的小长方形长和宽分别为x、y，剪去的两个小直角三角形的两直角边长也分别为x、y．