题目内容
1.观察下列各数:1,1,$\frac{5}{7}$,$\frac{7}{15}$,$\frac{9}{31}$,…按你发现的规律计算这列数的第7个数为( )| A. | $\frac{15}{255}$ | B. | $\frac{13}{127}$ | C. | $\frac{11}{127}$ | D. | $\frac{11}{63}$ |
分析 把前面的1,分别写成:$\frac{1}{1}$和$\frac{3}{3}$即可发现这列数的分子为奇数排列,而分母恰是2n-1,把n=7代入即可的得解.
解答 解:1,1,$\frac{5}{7}$,$\frac{7}{15}$,$\frac{9}{31}$,…整理为
$\frac{1}{1}$,$\frac{3}{3}$,$\frac{5}{7}$,$\frac{7}{15}$,$\frac{9}{31}$,…
可发现这列数的分子为奇数排列用2n-1表示,而分母恰是2n-1,
当n=7时,2n-1=13,2n-1=127,
所以这列数的第7个数为:$\frac{13}{127}$,
故选B.
点评 此题主要考查数列的规律探索问题,熟悉常见数列并用n表示其中的规律是解题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
13.在Rt△ABC中,∠C=90°,BC=6,AC=8,则cos∠BAC等于( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
11.下列各数中,最小的数是( )
| A. | -3 | B. | 1 | C. | 0 | D. | 2 |
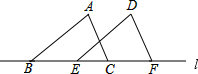 已知△ABC的边在直线l上,BC=5,现把△ABC沿着直线l向右平移到△DEF的位置(如图所示),若EC=3,则△ABC平移的距离为( )
已知△ABC的边在直线l上,BC=5,现把△ABC沿着直线l向右平移到△DEF的位置(如图所示),若EC=3,则△ABC平移的距离为( ) 如图,△ABC在方格中位置如图所示,A(1,4),B(-2,2).
如图,△ABC在方格中位置如图所示,A(1,4),B(-2,2).