题目内容
16.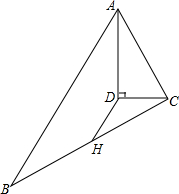 已知:如图,∠BAD=∠CAD,AB>AC,CD⊥AD于点D,H是BC中点.求证:DH=$\frac{1}{2}$(AB-AC).
已知:如图,∠BAD=∠CAD,AB>AC,CD⊥AD于点D,H是BC中点.求证:DH=$\frac{1}{2}$(AB-AC).
分析 延长CD交AB于E,证明△EAD≌△CAD,根据三角形中位线定理证明结论.
解答 证明: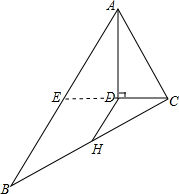 延长CD交AB于E,
延长CD交AB于E,
在△EAD和△CAD中,
$\left\{\begin{array}{l}{∠EAD=∠CAD}\\{AD=AD}\\{∠ADE=∠ADC}\end{array}\right.$,
∴△EAD≌△CAD,
∴AE=AC,ED=DC,
∵ED=DC,BH=HC,
∴DH=$\frac{1}{2}$BE,
∴DH=$\frac{1}{2}$(AB-AE)=$\frac{1}{2}$(AB-AC).
点评 本题考查的是三角形全等的判定和三角形中位线定理的应用,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.

练习册系列答案
相关题目
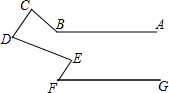 如图所示,已知CD∥EF,∠C+∠F=∠ABC,求证:AB∥GF.
如图所示,已知CD∥EF,∠C+∠F=∠ABC,求证:AB∥GF.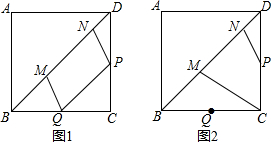
 如图,在?ABCD中,AE⊥BD于点E,CF⊥BD于点F,G、H分别为AD、BC的中点.求证:EF、GH互相平分.
如图,在?ABCD中,AE⊥BD于点E,CF⊥BD于点F,G、H分别为AD、BC的中点.求证:EF、GH互相平分.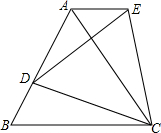 如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边△CDE,使点E、A在直线DC的同侧,连接AE,判断AE与BC的位置关系,并说明理由.
如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边△CDE,使点E、A在直线DC的同侧,连接AE,判断AE与BC的位置关系,并说明理由.