题目内容
7.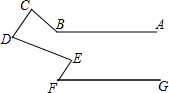 如图所示,已知CD∥EF,∠C+∠F=∠ABC,求证:AB∥GF.
如图所示,已知CD∥EF,∠C+∠F=∠ABC,求证:AB∥GF.
分析 延长CD交直线GF于M,延长FE交直线AB于N,直线AB和CD交于Q,根据三角形外角性质求出∠C+∠CQB=∠ABC,求出∠CQB=∠EFG,根据平行线的性质得出∠CQB=∠QNF,求出∠QNF=∠EFG,根据平行线的判定得出即可.
解答 证明:
延长CD交直线GF于M,延长FE交直线AB于N,直线AB和CD交于Q,如图,
∵∠C+∠CQB=∠ABC,∠C+∠EFG=∠ABC,
∴∠CQB=∠EFG,
∵CD∥EF,
∴∠CQB=∠QNF,
∴∠QNF=∠EFG,
∴AB∥GF.
点评 本题考查了三角形外角性质,平行线的性质和判定的应用,能正确作出辅助线是解此题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
17. 如图,在?ABCD中,AC、BD相交于点O,点E是AB的中点,OE=2cm,则AD的长是( )
如图,在?ABCD中,AC、BD相交于点O,点E是AB的中点,OE=2cm,则AD的长是( )
 如图,在?ABCD中,AC、BD相交于点O,点E是AB的中点,OE=2cm,则AD的长是( )
如图,在?ABCD中,AC、BD相交于点O,点E是AB的中点,OE=2cm,则AD的长是( )| A. | 1cm | B. | 2cm | C. | 3cm | D. | 4cm |
19.多项式25(m2+n2)2-16(m2-n2)2因式分解的结果是( )
| A. | (9m2+n2)(9n2+m2) | B. | (3m2+n2)(m+3n)(m-3n) | ||
| C. | (9m2+n)(3m-m)(3n-m) | D. | (3m+n)(3m-n)(3n+m)(3n-m) |
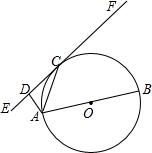 如图,AB是⊙O直径,EF切⊙O于C,AD⊥EF于D,求证:AC2=AD•AB.
如图,AB是⊙O直径,EF切⊙O于C,AD⊥EF于D,求证:AC2=AD•AB.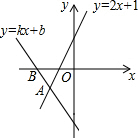 如图,直线y=kx+b与直线y=2x+1相交于点A(-1,-1),则不等式kx+b<2x+1<0的解集为x<-1-1<x<-$\frac{1}{2}$.
如图,直线y=kx+b与直线y=2x+1相交于点A(-1,-1),则不等式kx+b<2x+1<0的解集为x<-1-1<x<-$\frac{1}{2}$.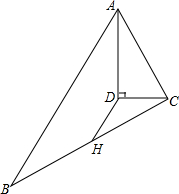 已知:如图,∠BAD=∠CAD,AB>AC,CD⊥AD于点D,H是BC中点.求证:DH=$\frac{1}{2}$(AB-AC).
已知:如图,∠BAD=∠CAD,AB>AC,CD⊥AD于点D,H是BC中点.求证:DH=$\frac{1}{2}$(AB-AC).