题目内容
20.已知不等式x-5≥2x+a的解集是x≤6,则直线y=x-5与y=2x+a的交点坐标是(6,1).分析 已知不等式的解集为x≤6,即当x<6时,y=x-5的函数值大于y=2x+a的函数值;由此可知,两函数图象的交点横坐标为x=6;代入y=x-5中,即可求出交点坐标.
解答 解:∵不等式x-5≥2x+a的解集是x≤6,
∴直线y=x-5与y=2x+a的交点的横坐标为6,
∵x=6时,y=x-5=1,
∴直线y=x-5与y=2x+a的交点坐标为(6,1).
故答案为(6,1).
点评 本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
相关题目
11.若x1,x2是x2-x-3=0的两个实数根,则-x1-x2=( )
| A. | ±1 | B. | -3 | C. | -1 | D. | 3 |
8.某瓷砖厂设计了几种瓷砖方案.如图所示,其中是轴对称图形的个数是( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
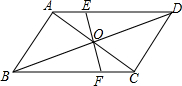 如图,?ABCD的对角线AC,BD相交于点O,EF经过点O且与AD,BC分别交于点E,F,已知AB=4,BC=5,OE=1.
如图,?ABCD的对角线AC,BD相交于点O,EF经过点O且与AD,BC分别交于点E,F,已知AB=4,BC=5,OE=1.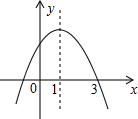 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论: