题目内容
7.小英与她的父亲、母亲计划外出旅游,初步选择了延安、西安、汉中、安康四个城市,由于时间仓促,他们只能去其中一个城市,到底去哪一个城市三人意见不统一,在这种情况下,小英父亲建议,用小英学过的摸球游戏来决定,规则如下:①在一个不透明的袋子中装一个红球(延安)、一个白球(西安)、一个黄球(汉中)和一个黑球(安康),这四个球除颜色不同外,其余完全相同;
②小英父亲先将袋中球摇匀,让小英从袋中随机摸出一球,父亲记录下其颜色,并将这个球放回袋中摇匀,然后让小英母亲从袋中随机摸出一球,父亲记录下它的颜色;
③若两人所摸出球的颜色相同,则去该球所表示的城市旅游.否则,前面的记录作废,按规则②重新摸球,直到两人所摸出球的颜色相同为止.
按照上面的规则,请你解答下列问题:
(1)已知小英的理想旅游城市是西安,小英和母亲随机各摸球一次,均摸出白球的概率是多少?
(2)已知小英母亲的理想旅游城市是汉中,小英和母亲随机各摸球一次,至少有一人摸出黄球的概率是多少?
分析 (1)先画状图展示所有16种等可能的结果数,再找出小英和母亲随机各摸球一次,均摸出白球的结果数,然后根据概率公式计算;
(2)找出小英和母亲随机各摸球一次,至少有一人摸出黄球的结果数,然后根据概率公式计算.
解答 解:(1)画树状图为:
共有16种等可能的结果数,其中小英和母亲随机各摸球一次,均摸出白球的结果数为1,
所以小英和母亲随机各摸球一次,均摸出白球的概率=$\frac{1}{16}$;
(2)小英和母亲随机各摸球一次,至少有一人摸出黄球的结果数为7,
所以小英和母亲随机各摸球一次,至少有一人摸出黄球的概率=$\frac{7}{16}$.
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.

练习册系列答案
相关题目
15. 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且AB=4,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为5,当GE+FH的值最大时,弦BC的长等于( )
如图,AB是⊙O的一条弦,点C是⊙O上一动点,且AB=4,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为5,当GE+FH的值最大时,弦BC的长等于( )
 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且AB=4,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为5,当GE+FH的值最大时,弦BC的长等于( )
如图,AB是⊙O的一条弦,点C是⊙O上一动点,且AB=4,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为5,当GE+FH的值最大时,弦BC的长等于( )| A. | 8 | B. | 10 | C. | 2$\sqrt{21}$或8 | D. | 2$\sqrt{21}$或10 |
2.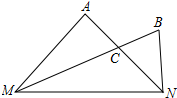 如图,在MN的同侧作△AMN和△BMN,BM平分∠AMN,AN平分∠BNM,AN交BM于点C.设∠A=α°,∠B=β°,下列结论不正确的是( )
如图,在MN的同侧作△AMN和△BMN,BM平分∠AMN,AN平分∠BNM,AN交BM于点C.设∠A=α°,∠B=β°,下列结论不正确的是( )
 如图,在MN的同侧作△AMN和△BMN,BM平分∠AMN,AN平分∠BNM,AN交BM于点C.设∠A=α°,∠B=β°,下列结论不正确的是( )
如图,在MN的同侧作△AMN和△BMN,BM平分∠AMN,AN平分∠BNM,AN交BM于点C.设∠A=α°,∠B=β°,下列结论不正确的是( )| A. | 若α=β,则点C在MN的垂直平分线上 | |
| B. | 若α+β=180°,则∠AMB=∠NMB | |
| C. | ∠MCN=$(\frac{α+β}{3}+60)$° | |
| D. | 当∠MCN=120°时,延长MA、NB交于点O,则OA=OB |
12.一个三角形的两边长为4和6,第三边的边长是方程(x-2)(x-5)=0的根,则这个三角形的周长为( )
| A. | 12 | B. | 15 | C. | 12或15 | D. | 以上都不对 |
16. 如图,设数轴上的点A,B,C表示的数分别为a,b,c,则下列说法中错误的是( )
如图,设数轴上的点A,B,C表示的数分别为a,b,c,则下列说法中错误的是( )
 如图,设数轴上的点A,B,C表示的数分别为a,b,c,则下列说法中错误的是( )
如图,设数轴上的点A,B,C表示的数分别为a,b,c,则下列说法中错误的是( )| A. | a<0 | B. | b>0 | C. | c>b | D. | a-b>0 |
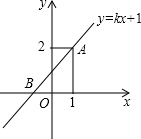 如图,一次函数y=kx+1的图象过点A(1,2),且与x轴相交于点B.若点P是坐标轴上的一点,且满足∠APB=90°,则点P的坐标是P1(1,0),P2(0,1+$\sqrt{2}$),P3(0,1-$\sqrt{2}$).
如图,一次函数y=kx+1的图象过点A(1,2),且与x轴相交于点B.若点P是坐标轴上的一点,且满足∠APB=90°,则点P的坐标是P1(1,0),P2(0,1+$\sqrt{2}$),P3(0,1-$\sqrt{2}$). 浠水县某中学规划在校园内一块长36米,宽20米的矩形场地ABCD上修建三条同样宽的人行道,使其中两条与AB平行,另一条与AD平行,其余部分种草,(如图所示),若使每一块草坪的面积都为96平方米,则人行道的宽为多少米?
浠水县某中学规划在校园内一块长36米,宽20米的矩形场地ABCD上修建三条同样宽的人行道,使其中两条与AB平行,另一条与AD平行,其余部分种草,(如图所示),若使每一块草坪的面积都为96平方米,则人行道的宽为多少米?