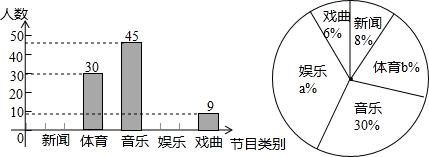
题目内容
19.已知AB是⊙O的直径,点P是直径AB上任意一点,过点P作弦CD⊥AB,垂足为点P,过B点的直线与线段AB的延长线交于点F,且∠F=∠ABC.
(1)如图1,求证:直线BF是⊙O的切线;
(2)如图2,当点P与点O重合时,过点A作⊙O的切线交线段BC的延长线于点E,在其它条件不变的情况下,判断四边形AEBF是什么特殊的四边形?证明你的结论.
分析 (1)欲证明直线BF是⊙O的切线,只要证明∠ABF=90°.
(2)结论四边形AEBF是平行四边形,只要证明AE∥BF,AF∥BE即可.
解答 (1)证明:如图1中,∵∠A=∠C,∠F=∠ABC,
∴∠ABF=∠CPB,
∵CD⊥AB,
∴∠ABF=∠CPB=90°,
∴直线BF是⊙O的切线.
(2)结论:四边形AEBF是平行四边形.
证明:如图2中,连接AC、BD.
∵OA=OB,
∴OC=OD,
∴四边形ACBD是平行四边形
∴AD∥BC,
即AF∥BE,
又∵AE切⊙O于点A,
∴AE⊥AB,
同理BF⊥AB,
∴AE∥BF,
∴四边形AEBF是平行四边形.
点评 本题考查切线的判定和性质、平行四边形的判定和性质等知识,解题的关键是灵活应用这些知识解决问题,属于中考常考题型.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
10.把0.00065用科学记数法表示为( )
| A. | -6.5×103 | B. | 0.65×10-3 | C. | -6.5×104 | D. | 6.5×10-4 |
4.若x2+kxy+16y2是一个完全平方式,那么k的值为( )
| A. | 4 | B. | 8 | C. | ±8 | D. | ±16 |
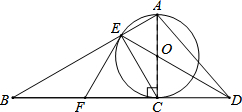 如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.
如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.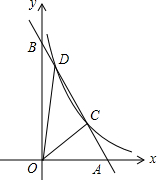 如图,已知直线y1=ax+b与x轴、y轴分别交于A、B两点,与双曲线y2=$\frac{k}{x}$(x>0)交于C(m,n)、D(p,q)两点,连接OC、OD.
如图,已知直线y1=ax+b与x轴、y轴分别交于A、B两点,与双曲线y2=$\frac{k}{x}$(x>0)交于C(m,n)、D(p,q)两点,连接OC、OD.