Question

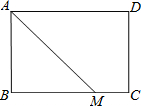如图，矩形ABCD中，AB=2

2

，AD=4，M点为线段BC上一个动点，连AM，N点为线段AM上一点，若△NCD为等腰三角形，且满足条件的N点有且只有三个，则线段BM的长为

 

．

Answer 1

考点：矩形的性质,等腰三角形的判定

专题：动点型

分析：若△NCD为等腰三角形，且满足条件的N点有且只有三个，则这三个点分别是CD的垂直平分线与AM的交点，以C为圆心以CD长为半径的圆与AM的交点，以D为圆心DC长为半径的圆与AM的切点，所以当DN=DC时，DN⊥AM，根据勾股定理求得AN=2

2

，然后求得△ABM≌△DNA，根据全等三角形的对应边相等得出BM=AN=2

2

．

解答：解：若△NCD为等腰三角形，且满足条件的N点有且只有三个，则这三个点分别是CD的垂直平分线与AM的交点，以C为圆心以CD长为半径的圆与AM的交点，以D为圆心DC长为半径的圆与AM的切点，
所以当DN=DC时，DN⊥AM，
∵四边形ABCD是矩形，
∴AD∥BC，AB=CD，
∵CD=DN，
∴AB=DN，
∴∠DAN=∠AMB，
∵∠B=∠AND=90°，
在△ABM与△DNA中

∠DAN=∠AMB ∠B=∠AND=90° AB=DN

∴△ABM≌△DNA（AAS），
∴BM=AN，
∵DN=DC=AB=2

2

，AD=4，
∴AN=

AD2-DN2

=2

2

，
∴BM=2

2

；
故答案为2

2

．

点评：本题考查了矩形的性质、等腰三角形的判定和性质、勾股定理的应用、三角形全等的判定和性质以及圆的切线的性质等，本题关键是当DN=DC时，DN⊥AM；