题目内容
14.三角形的三边长分别为a,b,c,若M=c2,N=a2+2ab+b2,则M-N的值( )| A. | 正数 | B. | 负数 | C. | 正数或0 | D. | 负数或0 |
分析 根据完全平方公式和平方差公式对要求的式子进行因式分解,再根据三角形的三边关系得出c+a+b>0,c-a-b<0,从而得出M-N的值.
解答 解:∵M=c2,N=a2+2ab+b2,
∴M-N=c2-(a2+2ab+b2)=c2-(a+b)2=(c+a+b)(c-a-b),
∵a,b,c是三角形的三边长,
∴c+a+b>0,c-a-b<0,
∴M-N的值负数;
故选B.
点评 此题考查了因式分解的应用,用到的知识点是三角形的三边关系、完全平方公式和平方差公式,根据三角形的三边关系得出c+a+b>0,c-a-b<0是本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4. 如图,△ABC中,∠C=90°,CD⊥AB于D,图中线段中可以作为△ACD的高的有( )
如图,△ABC中,∠C=90°,CD⊥AB于D,图中线段中可以作为△ACD的高的有( )
 如图,△ABC中,∠C=90°,CD⊥AB于D,图中线段中可以作为△ACD的高的有( )
如图,△ABC中,∠C=90°,CD⊥AB于D,图中线段中可以作为△ACD的高的有( )| A. | 0条 | B. | 1条 | C. | 2条 | D. | 3条 |
5.已知,在△ABC中,AD为BC边上的中线,AC=5,AD=4,则AB的取值范围是( )
| A. | 1<AB<9 | B. | 3<AB<13 | C. | 5<AB<13 | D. | 9<AB<13 |
2.在算式(-2)□(-3)的□中填上运算符号,使结果最小,运算符号是( )
| A. | 加号 | B. | 减号 | C. | 乘号 | D. | 除号 |
9.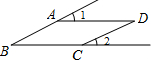 如图,∠1=∠B,∠2=25°,则∠D等于( )
如图,∠1=∠B,∠2=25°,则∠D等于( )
 如图,∠1=∠B,∠2=25°,则∠D等于( )
如图,∠1=∠B,∠2=25°,则∠D等于( )| A. | 25° | B. | 30° | C. | 45° | D. | 50° |
6. 直线a,b,c,d的位置如图所示,若∠1=∠2=90°,∠3=42°,那么∠4等于( )
直线a,b,c,d的位置如图所示,若∠1=∠2=90°,∠3=42°,那么∠4等于( )
 直线a,b,c,d的位置如图所示,若∠1=∠2=90°,∠3=42°,那么∠4等于( )
直线a,b,c,d的位置如图所示,若∠1=∠2=90°,∠3=42°,那么∠4等于( )| A. | 130° | B. | 138° | C. | 140° | D. | 142° |
3. 如图,每个小正方形的边长都为1,A、B、C是小正方形各顶点,则∠ABC的度数为( )
如图,每个小正方形的边长都为1,A、B、C是小正方形各顶点,则∠ABC的度数为( )
 如图,每个小正方形的边长都为1,A、B、C是小正方形各顶点,则∠ABC的度数为( )
如图,每个小正方形的边长都为1,A、B、C是小正方形各顶点,则∠ABC的度数为( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |

