题目内容
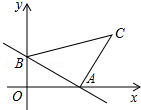 如图,一次函数y=-
如图,一次函数y=-| 3 |
| 4 |
考点:全等三角形的判定与性质,待定系数法求一次函数解析式,等腰直角三角形
专题:
分析:先根据一次函数的解析式求出A、B两点的坐标,再作CD⊥x轴于点D,由全等三角形的判定定理可得出△ABO≌△CAD,由全等三角形的性质可知OA=CD,故可得出C点坐标,再用待定系数法即可求出直线BC的解析式.
解答: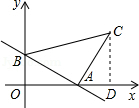 解:∵一次函数y=-
解:∵一次函数y=-
x+3中,
令x=0得:y=3;令y=0,解得x=4,
∴B的坐标是(0,3),A的坐标是(4,0).
如图,作CD⊥x轴于点D.
∵∠BAC=90°,
∴∠OAB+∠CAD=90°,
又∵∠CAD+∠ACD=90°,
∴∠ACD=∠BAO.
在△ABO与△CAD中,
,
∴△ABO≌△CAD(AAS),
∴OB=AD=3,OA=CD=4,OD=OA+AD=7.
则C的坐标是(7,4).
设直线BC的解析式是y=kx+b(k≠0),
根据题意得:
,
解得
,
∴直线BC的解析式是y=
x+3.
故答案是:y=
x+3.
 解:∵一次函数y=-
解:∵一次函数y=-| 3 |
| 4 |
令x=0得:y=3;令y=0,解得x=4,
∴B的坐标是(0,3),A的坐标是(4,0).
如图,作CD⊥x轴于点D.
∵∠BAC=90°,
∴∠OAB+∠CAD=90°,
又∵∠CAD+∠ACD=90°,
∴∠ACD=∠BAO.
在△ABO与△CAD中,
|
∴△ABO≌△CAD(AAS),
∴OB=AD=3,OA=CD=4,OD=OA+AD=7.
则C的坐标是(7,4).
设直线BC的解析式是y=kx+b(k≠0),
根据题意得:
|
解得
|
∴直线BC的解析式是y=
| 1 |
| 7 |
故答案是:y=
| 1 |
| 7 |
点评:本题考查的是一次函数综合题,涉及到用待定系数法求一次函数的解析式、全等三角形的判定与性质,根据题意作出辅助线,构造出全等三角形是解答此题的关键.

练习册系列答案
相关题目
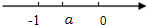 实数a在数轴上的位置如图,则a,-a,
实数a在数轴上的位置如图,则a,-a,| 1 |
| a |
A、a<-a<
| ||
B、-a<
| ||
C、
| ||
D、
|
 如图,?ABCD的周长是36cm,AB=8cm,BC=
如图,?ABCD的周长是36cm,AB=8cm,BC=