题目内容
15.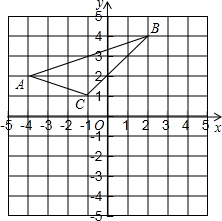 如图,在平面直角坐标系中,A(-4,2),B(2,4),C(-1,1).若将三角形ABC平移至三角形A1B1C1的位置时A1的坐标为(-2,-3).
如图,在平面直角坐标系中,A(-4,2),B(2,4),C(-1,1).若将三角形ABC平移至三角形A1B1C1的位置时A1的坐标为(-2,-3).(1)写出平移后的点B1,C1的坐标;
(2)在坐标系中画出平移后的三角形A1B1C1.
分析 (1)利用A点的平移规律,横坐标加2,纵坐标减5,进而得出点B1,C1的坐标;
(2)利用(1)中所求得出平移后的三角形A1B1C1.
解答  解:(1)∵A(-4,2),将三角形ABC平移至三角形A1B1C1的位置时A1的坐标为(-2,-3),
解:(1)∵A(-4,2),将三角形ABC平移至三角形A1B1C1的位置时A1的坐标为(-2,-3),
∴B(2,4),C(-1,1)分别平移后对应点的坐标为:B1(4,-1),C1(1,-4);
(2)如图所示:△A1B1C1,即为所求.
点评 此题主要考查了平移变换,根据题意得出A点平移规律是解题关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
17.为加快新农村试点示范建设,我省开展了“美丽乡村”的评选活动,下表是我省六个州(市)推荐候选的“美丽乡村”个数统计结果:
在上表统计的数据中,平均数和中位数分别为( )
| 州(市) | A | B | C | D | E | F |
| 推荐数(个) | 36 | 27 | 31 | 56 | 48 | 54 |
| A. | 42,43.5 | B. | 42,42 | C. | 31,42 | D. | 36,54 |
10.下列算式正确的是( )
| A. | -$\sqrt{(-3)^{2}}$=-3 | B. | (-$\sqrt{6}$)2=36 | C. | $\sqrt{16}$=±4 | D. | -(-$\sqrt{\frac{4}{9}}$)2=$\frac{4}{9}$ |
20.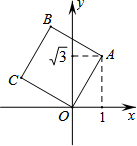 如图,将正方形OABC放在平面直角坐标系xOy中,O是原点,若点A的坐标为(1,$\sqrt{3}$),则点C的坐标为( )
如图,将正方形OABC放在平面直角坐标系xOy中,O是原点,若点A的坐标为(1,$\sqrt{3}$),则点C的坐标为( )
 如图,将正方形OABC放在平面直角坐标系xOy中,O是原点,若点A的坐标为(1,$\sqrt{3}$),则点C的坐标为( )
如图,将正方形OABC放在平面直角坐标系xOy中,O是原点,若点A的坐标为(1,$\sqrt{3}$),则点C的坐标为( )| A. | ($\sqrt{3}$,1) | B. | (-1,$\sqrt{3}$) | C. | (-$\sqrt{3}$,1) | D. | (-$\sqrt{3}$,-1) |
4.一个直角三角形有两条边分别是3cm、4cm,则第三条边的长度是( )
| A. | 5cm | B. | $\sqrt{7}$cm | C. | 5cm或$\sqrt{7}$cm | D. | 以上都不对 |
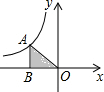 如图,点A在反比例函数y=$\frac{k}{x}$的图象上,AB垂直x轴于点B.若S△AOB=4,则这个反比例函数的解析式为y=-$\frac{8}{x}$.
如图,点A在反比例函数y=$\frac{k}{x}$的图象上,AB垂直x轴于点B.若S△AOB=4,则这个反比例函数的解析式为y=-$\frac{8}{x}$.