题目内容
在平面直角坐标系中,直线l1过点(2,3)和(-1,-3),直线l2过原点且与l1相交于点(-2,a).
(1)求a的值及直线l1,l2对应的函数表达式;
(2)设直线l1与l2交点为P,直线l1与y轴相交于点A,求△APO的面积.
(1)求a的值及直线l1,l2对应的函数表达式;
(2)设直线l1与l2交点为P,直线l1与y轴相交于点A,求△APO的面积.
考点:两条直线相交或平行问题
专题:
分析:(1)设直线l1的表达式为y=kx+b,然后利用待定系数法求一次函数解析式解答即可;再把交点坐标代入函数解析式求出a的值;设l2的解析式为y=mx,利用待定系数法求正比例函数解析式解答;
(2)根据(1)中a的值写出交点坐标即可,令x=0求出OA的长,再根据三角形的面积公式列式计算即可得解.
(2)根据(1)中a的值写出交点坐标即可,令x=0求出OA的长,再根据三角形的面积公式列式计算即可得解.
解答:解:(1)设直线l1的表达式为y=kx+b,
∵直线l1过点(2,3)和(-1,-3),
∴
,
解得
.
∴直线l1的函数表达式y=2x-1,
∵直线l2与l1相交于点(-2,a),
∴a=2×(-2)-1=-4-1=-5,
设l2的解析式为y=mx,
则-2m=-5,
解得m=
.
所以,l2的解析式为y=
x;
(2)∵a=-5,
∴直线l1与l2交点为P(2,-5),
令x=0,则y=-1,
∴OA=1,
∴点A的坐标为(0,-1),
∴△APO的面积=
×1×2=1.
∵直线l1过点(2,3)和(-1,-3),
∴
|
解得
|
∴直线l1的函数表达式y=2x-1,
∵直线l2与l1相交于点(-2,a),
∴a=2×(-2)-1=-4-1=-5,
设l2的解析式为y=mx,
则-2m=-5,
解得m=
| 5 |
| 2 |
所以,l2的解析式为y=
| 5 |
| 2 |
(2)∵a=-5,
∴直线l1与l2交点为P(2,-5),
令x=0,则y=-1,
∴OA=1,
∴点A的坐标为(0,-1),
∴△APO的面积=
| 1 |
| 2 |
点评:本题考查了两直线相交的问题,待定系数法求一次函数解析式,三角形的面积,求出直线l1的解析式,然后求出a的值是解题的关键.

练习册系列答案
相关题目
[-8(a-3b)5(3a+b)6]÷[-2(a-3b)(3a+b)2]的计算结果为( )
| A、4(a-3b)4(3a+b)3 | ||
| B、-4(a-3b)5(3a+b)4 | ||
C、
| ||
| D、4(a-3b)4(3a+b)4 |
 B,与y轴相交于点C,抛物线的对称轴与x轴相交于点M,点P是在y轴正半轴上的一个动点(点P、M、N不在同一条直线上).分别过点A、B作直线NP的垂线,垂足分别为E、F,连接ME、MF.
B,与y轴相交于点C,抛物线的对称轴与x轴相交于点M,点P是在y轴正半轴上的一个动点(点P、M、N不在同一条直线上).分别过点A、B作直线NP的垂线,垂足分别为E、F,连接ME、MF. 如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E,且AB=8,AD=4.P为线段AC上的任意一点,PG⊥AE于G,PH⊥EC于H,则PG+PH的值为
如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E,且AB=8,AD=4.P为线段AC上的任意一点,PG⊥AE于G,PH⊥EC于H,则PG+PH的值为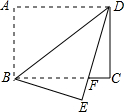 如图,在长方形ABCD中,AB∥CD,AD∥BC,AB=3,BC=4,将矩形纸片沿BD折叠,使点A落在点E处.设DE与BC相交于点F,
如图,在长方形ABCD中,AB∥CD,AD∥BC,AB=3,BC=4,将矩形纸片沿BD折叠,使点A落在点E处.设DE与BC相交于点F, 抛物线y=
抛物线y=