题目内容
腰长为2,底角为30°的等腰三角形的面积是 .
考点:含30度角的直角三角形,等腰三角形的性质,勾股定理
专题:
分析:作出图形,过点A作AD⊥BC于D,根据等腰三角形三线合一的性质可得BC=2BD,根据直角三角形30°角所对的直角边等于斜边的一半可得AD=
AB,再利用勾股定理列式求出BD,然后根据三角形的面积公式列式计算即可得解.
| 1 |
| 2 |
解答: 解:如图,过点A作AD⊥BC于D,
解:如图,过点A作AD⊥BC于D,
∵△ABC是等腰三角形,
∴BC=2BD,
∵底角∠B=30°,
∴AD=
AB=
×2=1,
由勾股定理得,BD=
=
=
,
∴BC=2
,
∴三角形的面积=
×2
×1=
.
故答案为:
.
 解:如图,过点A作AD⊥BC于D,
解:如图,过点A作AD⊥BC于D,∵△ABC是等腰三角形,
∴BC=2BD,
∵底角∠B=30°,
∴AD=
| 1 |
| 2 |
| 1 |
| 2 |
由勾股定理得,BD=
| AB2-AD2 |
| 22-12 |
| 3 |
∴BC=2
| 3 |
∴三角形的面积=
| 1 |
| 2 |
| 3 |
| 3 |
故答案为:
| 3 |
点评:本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质,等腰三角形三线合一的性质,熟记性质是解题的关键,作出图形更形象直观.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列各数中是无理数的是( )
| A、1 | ||
B、
| ||
| C、-2 | ||
D、
|
 如图所示,△ABC绕着点C顺时针旋转35°得到△A1B1C,若A1B1⊥AC,则∠A的度数是(
如图所示,△ABC绕着点C顺时针旋转35°得到△A1B1C,若A1B1⊥AC,则∠A的度数是(| A、35° | B、45° |
| C、55° | D、60° |
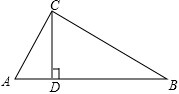 已知在△ABC中,CD⊥AB于D,由下列条件中的某一个就能推出△ABC是直角三角形的是
已知在△ABC中,CD⊥AB于D,由下列条件中的某一个就能推出△ABC是直角三角形的是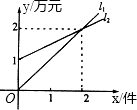 如图,l1表示某公司一种产品一天的销售收入与销售量的关系,l2表示该公司这种产品一天的销售成本与销售量的关系.
如图,l1表示某公司一种产品一天的销售收入与销售量的关系,l2表示该公司这种产品一天的销售成本与销售量的关系.